23. Uma loja colocou em promoção camisas, calças e malhas
de lã, sendo que qualquer peça do mesmo tipo tem o mesmo
preço.
Quatro amigos, Pedro, Paulo, Antônio e João foram a essa
loja e compraram:
Pedro: 2 camisas + 1 calça + 1 malha de lã e pagou R$ 330,00
Paulo: 3 camisas + 2 calças + 1malha de lã e pagou R$ 480,00
Antônio: 2 camisas + 1 calça + 2 malhas de lã e pagou
R$ 450,00.
Sabendo que João comprou apenas uma peça de cada tipo, o
valor pago por ele foi de
(A) R$ 270,00.
(B) R$ 280,00.
(C) R$ 290,00.
(D) R$ 300,00.
(E) R$ 310,00.


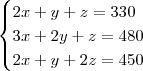


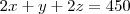


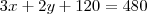

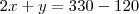
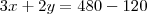




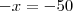



 .
.
 :
: