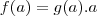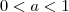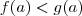por raimundoocjr » Dom Abr 28, 2013 12:01
por raimundoocjr » Dom Abr 28, 2013 12:01
01. (Adaptado) Determinar, no intervalo ]0,1[, se f(x)>g(x) ou g(x)>f(x). Sendo f(x)=
![\sqrt[]{x} \sqrt[]{x}](/latexrender/pictures/23c0d9674da78a0d1fae7f37c6ce8039.png)
e g(x)=
![\sqrt[3]{x} \sqrt[3]{x}](/latexrender/pictures/6833f4eaccfb60d5c13fdf6b6cc30aef.png)
.
Com a plotagem dos gráficos é fácil perceber que g(x)>f(x) no intervalo dado. Mas, de que maneira eu posso mostrar isso algebricamente?
-
raimundoocjr
-
 por young_jedi » Dom Abr 28, 2013 21:14
por young_jedi » Dom Abr 28, 2013 21:14
pensei no seguinte
vamos dizer que

sendo

então
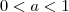
portanto temos que
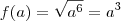
![g(a)=\sqrt[3]{a^3}=a^2 g(a)=\sqrt[3]{a^3}=a^2](/latexrender/pictures/361f3b47ccffc8ec55d4d22bca87a7af.png)
portanto

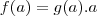
mais com
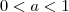
então
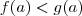
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (Calculo de trigonometria da UF-MS adaptado)
por andersontricordiano » Ter Dez 06, 2011 14:53
- 2 Respostas
- 1904 Exibições
- Última mensagem por sabaku

Ter Dez 06, 2011 23:26
Trigonometria
-
- [Função] Intervalo - Extremos
por raimundoocjr » Sáb Abr 27, 2013 19:48
- 0 Respostas
- 603 Exibições
- Última mensagem por raimundoocjr

Sáb Abr 27, 2013 19:48
Funções
-
- [Números inteiros no intervalo duma função]
 por Jhenrique » Dom Ago 26, 2012 20:33
por Jhenrique » Dom Ago 26, 2012 20:33
- 1 Respostas
- 1499 Exibições
- Última mensagem por Jhenrique

Qua Set 26, 2012 04:21
Funções
-
- Cáculo - Limites - função contínua num intervalo
por Antonio H V Araujo » Sáb Nov 14, 2015 22:24
- 1 Respostas
- 2573 Exibições
- Última mensagem por Cleyson007

Seg Nov 16, 2015 07:29
Cálculo: Limites, Derivadas e Integrais
-
- Intervalo
por Cristina Lins » Qua Abr 05, 2017 17:40
- 1 Respostas
- 3123 Exibições
- Última mensagem por petras

Qua Mai 03, 2017 21:03
Conjuntos
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[]{x} \sqrt[]{x}](/latexrender/pictures/23c0d9674da78a0d1fae7f37c6ce8039.png) e g(x)=
e g(x)=![\sqrt[3]{x} \sqrt[3]{x}](/latexrender/pictures/6833f4eaccfb60d5c13fdf6b6cc30aef.png) .
.
![\sqrt[]{x} \sqrt[]{x}](/latexrender/pictures/23c0d9674da78a0d1fae7f37c6ce8039.png) e g(x)=
e g(x)=![\sqrt[3]{x} \sqrt[3]{x}](/latexrender/pictures/6833f4eaccfb60d5c13fdf6b6cc30aef.png) .
.

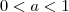
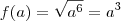
![g(a)=\sqrt[3]{a^3}=a^2 g(a)=\sqrt[3]{a^3}=a^2](/latexrender/pictures/361f3b47ccffc8ec55d4d22bca87a7af.png)