 por CarolMarques » Ter Abr 23, 2013 10:53
por CarolMarques » Ter Abr 23, 2013 10:53
Na Questão:
Devido a uma maldição rogada por uma tribo vizinha , os membros de uma aldeia são gradualmente impelidos ao assassinato ou ao suicidio.A taxa de variação da população é
![-2\sqrt[]{p} -2\sqrt[]{p}](/latexrender/pictures/e62d9fc67557e1086ffa8988011ef537.png)
pessoas por mes , quando o numero de pessoas é p.Quando a maldição foi rogada , a população era de 1600.Quando morrerá toda a população da aldeia?
Eu estou tendo dificuldade em questões de aplicações de EDO.Eu comoecei a questão assim:
dp(t)= - 2 raiz de p(t)
dt
E resolvi a EDO , mas não bateu com o gabarito que é 40 meses.Por favor me ajudem.
-
CarolMarques
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Qui Mai 03, 2012 20:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
 por young_jedi » Qui Abr 25, 2013 22:38
por young_jedi » Qui Abr 25, 2013 22:38
temso que
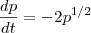
então
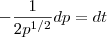
então temos que

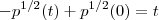
se a população inicial e 1600 então p(0)=1600 e no fim termina com 0 então p(t)=0
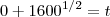
t=40
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvida Eq. Diferenciais 2ª Ordem - Ex. Aplicado
por daniel2678 » Qua Abr 27, 2011 02:14
- 2 Respostas
- 3224 Exibições
- Última mensagem por 0146251

Seg Mai 25, 2015 21:42
Cálculo: Limites, Derivadas e Integrais
-
- duvida para derivar a segunda ordem
por PORTER » Ter Nov 04, 2014 21:37
- 3 Respostas
- 3252 Exibições
- Última mensagem por Russman

Qua Nov 05, 2014 11:32
Cálculo: Limites, Derivadas e Integrais
-
- dúvida, derivar seno e cosseno até a terceira ordem
por PORTER » Qui Dez 11, 2014 08:10
- 1 Respostas
- 1348 Exibições
- Última mensagem por adauto martins

Sex Dez 12, 2014 11:34
Cálculo: Limites, Derivadas e Integrais
-
- Inversa de 3° Ordem
por DanielRJ » Sáb Set 11, 2010 15:34
- 2 Respostas
- 4846 Exibições
- Última mensagem por DanielRJ

Sáb Set 11, 2010 16:23
Matrizes e Determinantes
-
- EDO de Segunda Ordem
por OtavioBonassi » Ter Nov 15, 2011 11:45
- 0 Respostas
- 1258 Exibições
- Última mensagem por OtavioBonassi

Ter Nov 15, 2011 11:45
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![-2\sqrt[]{p} -2\sqrt[]{p}](/latexrender/pictures/e62d9fc67557e1086ffa8988011ef537.png) pessoas por mes , quando o numero de pessoas é p.Quando a maldição foi rogada , a população era de 1600.Quando morrerá toda a população da aldeia?
pessoas por mes , quando o numero de pessoas é p.Quando a maldição foi rogada , a população era de 1600.Quando morrerá toda a população da aldeia?

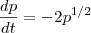
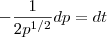

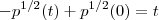
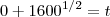



 , avisa que eu resolvo.
, avisa que eu resolvo.

