circunferência trigonométrica e que não esteja sobre
nenhum dos eixos coordenados. Seja
 o ângulo
o ângulo determinado pelo eixo OX e pela semi-reta OP, onde
O é a origem do sistema. Nessas condições, assinale
o que for correto.
01) A abscissa de P é menor do que cos(
 ).
).02) A ordenada de P é igual a sen[
 + (
+ ( /2)].
/2)].04) A tangente de
 é determinada pela razão entre a
é determinada pela razão entre a ordenada e a abscissa de P.
08) As coordenadas de P satisfazem à equação
 .
.16) Se x = y, então cotg(
 ) = -1.
) = -1.32)
 =
=  /4 é o menor arco positivo para o qual a
/4 é o menor arco positivo para o qual aequação
 (
( +
+  ) +
) +  [
[ + (
+ ( /2)] =
/2)] =  [(
[( +
+ (
 /2)] +
/2)] +  (
( +
+  ) é satisfeita.
) é satisfeita.64) sen(2
 ) = 2y.
) = 2y.Não entendi as partes do sen e cos, onde usa, ou seja toda a parte não entendi


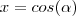
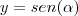
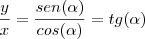
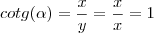


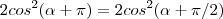
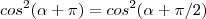
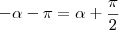
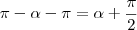
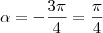
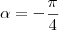
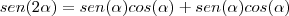
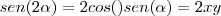



 , avisa que eu resolvo.
, avisa que eu resolvo.

