


 em
em ![[-4,4] [-4,4]](/latexrender/pictures/bdebec222f4aa38fc1bd1064c8e24fe4.png) temos que
temos que  .Ou seja , para cada
.Ou seja , para cada  em
em ![[-4,4] [-4,4]](/latexrender/pictures/bdebec222f4aa38fc1bd1064c8e24fe4.png) não existe um único
não existe um único  tal que
tal que 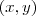 é solução da equação
é solução da equação  .
. ![x^2 +( \sqrt{16-x^2})^2 = x^2 + 16 - x^2 = [x^2 +(-x^2)] + 16 = 16 x^2 +( \sqrt{16-x^2})^2 = x^2 + 16 - x^2 = [x^2 +(-x^2)] + 16 = 16](/latexrender/pictures/958a949ee2585a4f102c0beadfec1f38.png) .
. ![x^2 +( -\sqrt{16-x^2})^2 = x^2 +( -1)^2 (\sqrt{16-x^2})^2 = x^2 + 16 - x^2 = [x^2 +(-x^2)] + 16 = 16 x^2 +( -\sqrt{16-x^2})^2 = x^2 +( -1)^2 (\sqrt{16-x^2})^2 = x^2 + 16 - x^2 = [x^2 +(-x^2)] + 16 = 16](/latexrender/pictures/44ec58ce9866a860fb372c8e2bc8c25e.png)

santhiago escreveu:Basta notar que para cadaem
temos que
.Ou seja , para cada
em
não existe um único
tal que
é solução da equação
.
De fato ,.
Por outro lado ,

 e extraiu a raiz quadrada de ambos membros obtendo que
e extraiu a raiz quadrada de ambos membros obtendo que 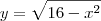 que na verdade o correto seria ficarmos com o módulo
que na verdade o correto seria ficarmos com o módulo  .Se
.Se  é solução da equação ,
é solução da equação ,  também o é .Pense sobre isto .
também o é .Pense sobre isto . e
e  temos que
temos que 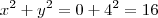 .Por outro lado ,se
.Por outro lado ,se  temos que
temos que  . Pense sobre isto .
. Pense sobre isto .
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes