 por Sohrab » Qui Abr 25, 2013 03:41
por Sohrab » Qui Abr 25, 2013 03:41
Pessoal, estou estudando quádricas e cilindros..
Uma questão pede para descrever e esboçar o gráfico de uma superfície
yz = 4
eu vi nas repostas, e é uma hipérbole (um cilindro hiperbólico, na verdade, já que o traço dessa hipérbole se repete para cada valor de x (cilindro paralelo ao eixo x))
mas não estou conseguindo entender porque, as interseções de yz = 4 com os planos x = k(constante) dão hipérbole no plano yz.. desde quando isso é uma equação de hipérbole?
por exemplo.. como vou achar os focos, centro, etc dessa hipérbole?
-
Sohrab
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Qui Mar 18, 2010 17:42
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: Téc. em Mec. Usinagem e Info Programação
- Andamento: cursando
 por LuizAquino » Qui Abr 25, 2013 19:17
por LuizAquino » Qui Abr 25, 2013 19:17
Sohrab escreveu:Pessoal, estou estudando quádricas e cilindros..
Uma questão pede para descrever e esboçar o gráfico de uma superfície
yz = 4
eu vi nas repostas, e é uma hipérbole (um cilindro hiperbólico, na verdade, já que o traço dessa hipérbole se repete para cada valor de x (cilindro paralelo ao eixo x))
mas não estou conseguindo entender porque, as interseções de yz = 4 com os planos x = k(constante) dão hipérbole no plano yz.. desde quando isso é uma equação de hipérbole?
por exemplo.. como vou achar os focos, centro, etc dessa hipérbole?
O seu problema é que você está querendo uma equação da hipérbole no formato padrão, ou seja, algo do tipo:
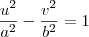
Mas acontece que se uma hipérbole está rotacionada em relação ao sistema de coordenadas, então aparecerá em sua equação um termo misto (ou termo cruzado), isto é, um termo do tipo uv. Para eliminar este termo, você precisa efetuar uma rotação de eixos, de modo que no novo sistema a hipérbole não esteja mais rotacionada.
Eu gostaria de sugerir que você assista a videoaula "33. Geometria Analítica - Rotação de Eixos". Eu espero que ela possa lhe ajudar a entender melhor o problema. Esta videoaula está disponível no curso de Geometria Analítica em minha página:
http://www.lcmaquino.org/
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Hiperbole
por Schimuneck » Seg Mai 30, 2011 10:21
- 1 Respostas
- 5730 Exibições
- Última mensagem por DanielFerreira

Sáb Mai 19, 2012 14:29
Geometria Analítica
-
- [Hipérbole]
por Ana_Rodrigues » Qua Nov 23, 2011 19:33
- 3 Respostas
- 4040 Exibições
- Última mensagem por MarceloFantini

Qua Nov 23, 2011 20:54
Geometria Analítica
-
- Hiperbole
por Claudin » Qui Mai 24, 2012 02:44
- 2 Respostas
- 1940 Exibições
- Última mensagem por Claudin

Ter Jun 12, 2012 20:31
Geometria Analítica
-
- Hiperbole
por Claudin » Qui Mai 24, 2012 02:47
- 2 Respostas
- 1765 Exibições
- Última mensagem por Claudin

Ter Jun 12, 2012 20:32
Geometria Analítica
-
- Hipérbole
por Claudin » Qui Mai 24, 2012 02:50
- 2 Respostas
- 1737 Exibições
- Última mensagem por Claudin

Ter Jun 12, 2012 20:32
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


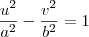



 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.