Suponha f contínua em [a,b].Seja g:[c,d]
IR com g' contínua em [c,d], g(c)=a e g(d)=b. Suponha ainda que g'(u)>0 em ]c,d[ .Seja c = u0<u1<u2<....<un=d uma partição de [c,d] e seja a= x0<x1<x2<...<xn = b partição de [a,b] onde xi = g(ui) para i variando de 0 a n.a) mostre que para todo i, i = 1,2,....n existe ui em [ui-1,ui] tal que
b) conclua de (a) que
onde ci = g(ui).c) Mostre que existe M>0 tal que
para i variando de 0 a n.d) conclua que
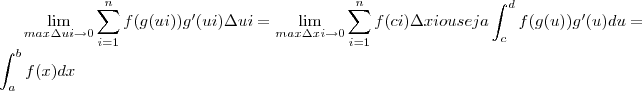
por ![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)