 por rochadapesada » Seg Abr 22, 2013 20:27
por rochadapesada » Seg Abr 22, 2013 20:27
Seja Z = cos? + i sen?, a representação trigonométrica do número complexo Z de módulo unitário, cujo argumento principal é ?, então...
As perguntas estão no anexo... Eu não conseguir fazer, pois sabendo da primeira resposta, dar para encontrar as outras... eu fiz desse jeito
0-0)
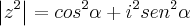
, então irá dar:

, pois

.... Mas como vi no gabarito ele mostra que irá dar uma adição e não subtração, e estou com duvida nisso... Ah a também não entendi em relação aos afixos... Como vi a última (4-4), queria saber o motivo que não se eleva ao quadrado o i, pois essa (4-4) está verdadeira, e na justificativa mostra que i não foi elevado
- Anexos
-

- Sem títulao.png (7.08 KiB) Exibido 1344 vezes
-
rochadapesada
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Abr 04, 2013 22:00
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- não consigo responder as questões de juros simles
por Fran » Seg Ago 10, 2009 14:37
- 2 Respostas
- 3914 Exibições
- Última mensagem por Fran

Qua Ago 12, 2009 13:38
Matemática Financeira
-
- Não consigo achar o limite
por CrazzyVi » Sáb Nov 14, 2009 13:34
- 2 Respostas
- 2491 Exibições
- Última mensagem por CrazzyVi

Qui Dez 10, 2009 14:28
Cálculo: Limites, Derivadas e Integrais
-
- Não consigo achar o determinante
por IsabelRangell » Qui Abr 08, 2010 17:08
- 1 Respostas
- 2502 Exibições
- Última mensagem por MarceloFantini

Qui Abr 08, 2010 19:55
Matrizes e Determinantes
-
- Nao consigo achar a forma reduzida da matriz..
por PeIdInHu » Seg Jun 14, 2010 23:07
- 1 Respostas
- 2572 Exibições
- Última mensagem por PeIdInHu

Seg Jun 14, 2010 23:55
Matrizes e Determinantes
-
- voce pode me ajudar,nao consigo achar a resposta
 por Dalila » Sex Nov 14, 2008 17:28
por Dalila » Sex Nov 14, 2008 17:28
- 1 Respostas
- 1671 Exibições
- Última mensagem por Molina

Sex Jun 12, 2009 20:56
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
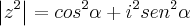 , então irá dar:
, então irá dar:  , pois
, pois  .... Mas como vi no gabarito ele mostra que irá dar uma adição e não subtração, e estou com duvida nisso... Ah a também não entendi em relação aos afixos... Como vi a última (4-4), queria saber o motivo que não se eleva ao quadrado o i, pois essa (4-4) está verdadeira, e na justificativa mostra que i não foi elevado
.... Mas como vi no gabarito ele mostra que irá dar uma adição e não subtração, e estou com duvida nisso... Ah a também não entendi em relação aos afixos... Como vi a última (4-4), queria saber o motivo que não se eleva ao quadrado o i, pois essa (4-4) está verdadeira, e na justificativa mostra que i não foi elevado
