Observe a figura :
Nela o círculo tem o centro O e raio 6 e OP=16. A reta PT é tangente ao circulo em T eo segmento --TQ é perpendicular á reta OP assim sendo, o comprimento do segmento QP é? da uma ajuda nesse exercicio...
R:13,75






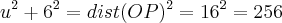
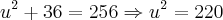
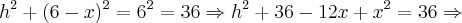
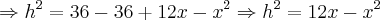
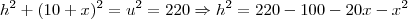
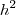 :
: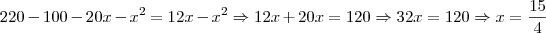


Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante


 , avisa que eu resolvo.
, avisa que eu resolvo.

