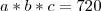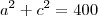por Daniel Gurgel » Qui Out 22, 2009 12:15
por Daniel Gurgel » Qui Out 22, 2009 12:15
Olá pessoal, não estou conseguindo fazer essa questão, se alguém conseguir mande-me a resolução por favor.
A área de um paralelepípedo retângulo é 720
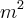
. A diagonal de uma de suas faces mede 20m e a soma das suas dimensões é 34m .Quais as dimensões deste paralelepípedo ?
-
Daniel Gurgel
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Sáb Ago 22, 2009 18:04
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: concursos
- Andamento: cursando
 por Molina » Qui Out 22, 2009 13:51
por Molina » Qui Out 22, 2009 13:51
Boa tarde, Daniel.
Temos três equações:
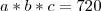

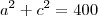
To tentando usar essas informações para encontrar alguma das dimensões.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Daniel Gurgel » Sáb Out 24, 2009 12:23
por Daniel Gurgel » Sáb Out 24, 2009 12:23
Eu tentei fazer assim:
2ab+2ac+2bc=720
a+b+c=34
aa+bb=400
Só que ñ consegui!
-
Daniel Gurgel
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Sáb Ago 22, 2009 18:04
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: concursos
- Andamento: cursando
Voltar para Geometria Espacial
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- paralelepipedo
por Gir » Ter Set 22, 2009 10:41
- 2 Respostas
- 6092 Exibições
- Última mensagem por Gir

Ter Set 22, 2009 15:32
Geometria Espacial
-
- Paralelepípedo
por vitoria » Qui Set 24, 2009 10:36
- 2 Respostas
- 1750 Exibições
- Última mensagem por vitoria

Qui Set 24, 2009 17:17
Geometria Espacial
-
- Volume do Paralelepípedo
por Vini » Ter Out 20, 2009 12:09
- 1 Respostas
- 3533 Exibições
- Última mensagem por Vini

Qui Out 22, 2009 12:07
Geometria Espacial
-
- paralelepipedo retangular
por pedro martins » Sáb Jun 02, 2012 15:37
- 0 Respostas
- 1547 Exibições
- Última mensagem por pedro martins

Sáb Jun 02, 2012 15:37
Geometria Espacial
-
- Volume do Paralelepípedo
por Santosk » Seg Abr 15, 2013 15:17
- 1 Respostas
- 1991 Exibições
- Última mensagem por young_jedi

Seg Abr 15, 2013 21:28
Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
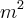 . A diagonal de uma de suas faces mede 20m e a soma das suas dimensões é 34m .Quais as dimensões deste paralelepípedo ?
. A diagonal de uma de suas faces mede 20m e a soma das suas dimensões é 34m .Quais as dimensões deste paralelepípedo ?
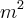 . A diagonal de uma de suas faces mede 20m e a soma das suas dimensões é 34m .Quais as dimensões deste paralelepípedo ?
. A diagonal de uma de suas faces mede 20m e a soma das suas dimensões é 34m .Quais as dimensões deste paralelepípedo ?