 por JessicaAraujo » Dom Abr 14, 2013 19:05
por JessicaAraujo » Dom Abr 14, 2013 19:05
Podem me ajudar?
Encontre o domínio de f(x)= sec(x/2) e resolva a inequação sec(x/2) > 2 para x ? [0,4?]
-
JessicaAraujo
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qui Abr 11, 2013 15:52
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por e8group » Dom Abr 14, 2013 19:32
por e8group » Dom Abr 14, 2013 19:32
Como
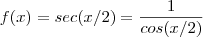
e
![x \in[0,4\pi] x \in[0,4\pi]](/latexrender/pictures/a63d22811bc082a2f57ab749279caf00.png)
,o domínio da função

será
![D_f = \{x \in[0,4\pi] : cos(x/2) \neq 0 \} D_f = \{x \in[0,4\pi] : cos(x/2) \neq 0 \}](/latexrender/pictures/ae7fda66d0687d797c14ad4a9aba2872.png)
.
Pergunta : Quais valores no intervalo
![[0,4\pi] [0,4\pi]](/latexrender/pictures/47d05e202385b396a7504deb9ff6631b.png)
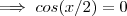
??
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Encontrar Domínio]
por JessicaAraujo » Ter Abr 16, 2013 22:00
- 1 Respostas
- 827 Exibições
- Última mensagem por young_jedi

Qua Abr 17, 2013 11:47
Funções
-
- [Encontrar domínio e imagem]
por Larry Crowne » Sex Mar 29, 2013 21:46
- 1 Respostas
- 959 Exibições
- Última mensagem por nakagumahissao

Sáb Mar 30, 2013 01:48
Funções
-
- Encontrar Dominio usando logaritimo
por barizom » Sáb Mar 27, 2010 13:58
- 2 Respostas
- 1935 Exibições
- Última mensagem por barizom

Sáb Mar 27, 2010 20:48
Funções
-
- dominio de uma função trigonometrica
por tigre matematico » Qua Out 19, 2011 20:02
- 5 Respostas
- 2708 Exibições
- Última mensagem por TheoFerraz

Qui Out 20, 2011 13:12
Funções
-
- Encontrar a Equação Geral do Plano
por Vitor2+ » Seg Nov 14, 2011 02:21
- 7 Respostas
- 10643 Exibições
- Última mensagem por LuizAquino

Qua Nov 16, 2011 15:04
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



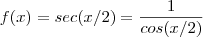 e
e ![x \in[0,4\pi] x \in[0,4\pi]](/latexrender/pictures/a63d22811bc082a2f57ab749279caf00.png) ,o domínio da função
,o domínio da função  será
será ![D_f = \{x \in[0,4\pi] : cos(x/2) \neq 0 \} D_f = \{x \in[0,4\pi] : cos(x/2) \neq 0 \}](/latexrender/pictures/ae7fda66d0687d797c14ad4a9aba2872.png) .
. ![[0,4\pi] [0,4\pi]](/latexrender/pictures/47d05e202385b396a7504deb9ff6631b.png)
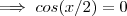 ??
??

 .
.
 :
: