por rochadapesada » Dom Abr 14, 2013 17:40
por rochadapesada » Dom Abr 14, 2013 17:40
Não conseguir fazer essa questão, eu deduzir que com a rotação iria ocorrer a formação de 3 cones, mas fazendo os cálculos não dar nenhum resultado =s
O volume do sólido gerado pela rotação do triângulo isósceles de 6 cm de altura e 2 cm de base em torno da base é, em

:
a)12

b)14

c)24

d)26

e)36

-
rochadapesada
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Abr 04, 2013 22:00
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por marciosouza » Dom Abr 14, 2013 17:55
por marciosouza » Dom Abr 14, 2013 17:55
Olá!
Deixa eu ver se consigo te ajudar!
Imagine se vc girar isso, ficaria com uma espécie de disco certo... de modo que o volume deste disco é a metade do volume gerado pelo cilindro que é obtido ao projetar as bases com seis cm de altura, o que te daria um retângulo de base 2 ( a mesma base do triângulo e altura 6 (conforme altura do triângulo... rotacionando este retângulo sobre a sua base (2) terás um cilindro... a metade dele te dará o volume que queres...
Resposta 24pi
-
marciosouza
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Ter Set 20, 2011 16:25
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por rochadapesada » Ter Abr 16, 2013 17:39
por rochadapesada » Ter Abr 16, 2013 17:39
Você falou e eu não entendi nadinha nadinha =s... não tem como mostrar por figura ou explicar de novo? Não entendi essa parte do disco nem a parte do cilindro
-
rochadapesada
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Abr 04, 2013 22:00
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Geometria Espacial
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Geometria Espacial] Rotação de um trapézio
 por rochadapesada » Dom Abr 14, 2013 17:49
por rochadapesada » Dom Abr 14, 2013 17:49
- 2 Respostas
- 6707 Exibições
- Última mensagem por rochadapesada

Ter Abr 16, 2013 18:07
Geometria Espacial
-
- [Geometria espacial] Prisma de base um triângulo equilátero
por rochadapesada » Seg Abr 08, 2013 18:13
- 1 Respostas
- 2890 Exibições
- Última mensagem por aleph

Ter Out 06, 2015 20:31
Geometria Espacial
-
- [Geometria Plana - Triângulo] Triângulo Isós. e Bissetriz
por raimundoocjr » Qua Fev 22, 2012 09:41
- 3 Respostas
- 6601 Exibições
- Última mensagem por DanielFerreira

Sáb Fev 25, 2012 01:37
Geometria Plana
-
- geometria espacial
por Gir » Seg Jul 27, 2009 11:46
- 3 Respostas
- 11735 Exibições
- Última mensagem por Molina

Ter Jul 28, 2009 15:21
Problemas do Cotidiano
-
- Geometria espacial
por nathy vieira » Qua Out 07, 2009 22:37
- 2 Respostas
- 2846 Exibições
- Última mensagem por nathy vieira

Qua Out 07, 2009 23:03
Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 :
:





 :
:







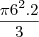 =
=