2^(x+2 )– 3 × 2^(x-1) =20
Pessoal, fiz de uma forma, mas quando fui substiuir no x, não deu o resultado esperado
4y- 3y/2 =20
8y-3y =20
y= 20/5
y=4
2^x=y
x=2
O que posso fazer?



 ???
???


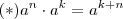 para todo
para todo 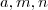 real e
real e 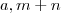 não simultaneamente nulo .(Isto por que esta regra não vale para
não simultaneamente nulo .(Isto por que esta regra não vale para  )
)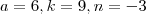 teremos
teremos  .
.  ;logo
;logo 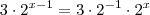 .
.  e responda :
e responda : 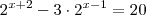 é equivalente a
é equivalente a  ???
???
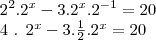
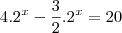

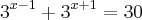
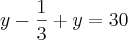

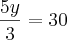


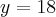



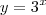 ,certo ? Acompanhe então o desenvolvimento .Temos a equação ,
,certo ? Acompanhe então o desenvolvimento .Temos a equação , 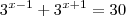 que devido a propriedade
que devido a propriedade  a equação pode ser escrita como
a equação pode ser escrita como 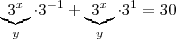 .(Dica: Tome
.(Dica: Tome  e
e 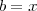 e
e  para aplicar a propriedade ).Além disso ,
para aplicar a propriedade ).Além disso , .Assim ,temos :
.Assim ,temos :  .Multiplicando ambos lados da equação por
.Multiplicando ambos lados da equação por  para eliminarmos a fração 1/3 ,segue
para eliminarmos a fração 1/3 ,segue 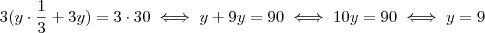 .Desta forma você encontra
.Desta forma você encontra  uma vez que
uma vez que  .
.


Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes