 por Cosma » Qui Abr 11, 2013 20:54
por Cosma » Qui Abr 11, 2013 20:54
Olá galera! Acabei de me inscrever aqui e necessito de ajuda para resolver algumas funções de primeiro grau. Receio que não tenha visto esse tema com a devida profundidade pois não faço ideia nem por onde começar. O exercício diz o seguinte:
É dado que f(x) > 0, para todo x real, f(1) = 3 e f(u + v) = f(u) . f(v), para quaisquer números reais u e v. Calcule:
a.) f(2)
b.) f(0)
c.) f(1/2)
Eu tentei montar algum tipo de sistema para achar valores de u e v, mas percebi que não é por ai que devo começar, pois fazendo
u + v = 1
u . v = 3
onde, v = 1 - u
e substituindo u . (1 - u) = 3
simplificando e resolvendo, eu chego na equação de segundo grau - u² + u - 3, onde o delta é negativo, não possuindo raízes reais.
Não faço ideia do que fazer, por favor, me ajudem =(
-
Cosma
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Abr 11, 2013 20:41
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por e8group » Qui Abr 11, 2013 21:53
por e8group » Qui Abr 11, 2013 21:53
Podemos Tomar

;assim

.
Como

,concluímos que
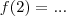
. Qual a resposta ?
E com respeito a

? Podemos tomar

e

;assim ,

,logo
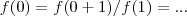
e qual seria a resposta ?
E
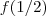
,como ficaria ??
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Russman » Qui Abr 11, 2013 23:41
por Russman » Qui Abr 11, 2013 23:41
A função que satisfaz essa propriedade
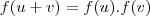
é a função exponencial! (:
Veja que se
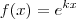
, onde

é uma constante real, temos então

Basta determinar o valor de

usando a informação

.

Portanto,

e então podemos determinar a função
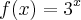
.
Agora basta substituir os valores de

e voce terá os valores das funções.
Claro que o método do amigo ali de cima é mais geral, mas eu achei que valia a pena ressaltar essa observação.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Cosma » Sáb Abr 13, 2013 12:37
por Cosma » Sáb Abr 13, 2013 12:37
Aah, entendi agora!
Tratando-se de uma função, podemos jogar valores para u e v e disso descobrimos a constante que é a função exponencial igual nosso amigo disse.
Se

e

a gente conclui que
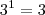
logo
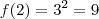
e
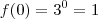
E o

seria, transformando em raiz ficaria
![\sqrt[2]{3} \sqrt[2]{3}](/latexrender/pictures/77529b271d4ed2ab8ca1f0755594aa28.png)
, correto?
-
Cosma
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Abr 11, 2013 20:41
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Russman » Sáb Abr 13, 2013 14:50
por Russman » Sáb Abr 13, 2013 14:50
Sim. As potências fracionárias são raízes.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Não sei nem por onde começar
por Daniel Bertuol » Ter Set 06, 2011 14:03
- 1 Respostas
- 1554 Exibições
- Última mensagem por Neperiano

Ter Set 06, 2011 14:47
Matemática Financeira
-
- Não sei nem por onde começar essa.....
por cidaiesbik » Seg Mai 04, 2009 12:51
- 2 Respostas
- 2665 Exibições
- Última mensagem por cidaiesbik

Seg Mai 04, 2009 18:22
Desafios Difíceis
-
- Dúvida não sei por onde começar...
por csmoreira » Seg Mar 04, 2013 20:46
- 0 Respostas
- 2341 Exibições
- Última mensagem por csmoreira

Seg Mar 04, 2013 20:46
Álgebra Linear
-
- função do segundo grau, urgente não sei como começar
por eri » Sex Mar 15, 2013 23:31
- 1 Respostas
- 3738 Exibições
- Última mensagem por XILVANA

Qua Abr 10, 2013 13:20
Funções
-
- Função de Primeiro Grau
por Najyh » Seg Mai 03, 2010 23:22
- 3 Respostas
- 5039 Exibições
- Última mensagem por MarceloFantini

Ter Mai 04, 2010 22:41
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 ;assim
;assim  .
.  ,concluímos que
,concluímos que 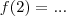 . Qual a resposta ?
. Qual a resposta ?  ? Podemos tomar
? Podemos tomar  e
e  ;assim ,
;assim ,  ,logo
,logo 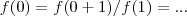 e qual seria a resposta ?
e qual seria a resposta ? 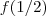 ,como ficaria ??
,como ficaria ??
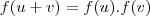
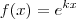 , onde
, onde  é uma constante real, temos então
é uma constante real, temos então

 e então podemos determinar a função
e então podemos determinar a função 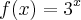 .
. e voce terá os valores das funções.
e voce terá os valores das funções. e
e 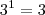
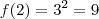
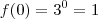
 seria, transformando em raiz ficaria
seria, transformando em raiz ficaria ![\sqrt[2]{3} \sqrt[2]{3}](/latexrender/pictures/77529b271d4ed2ab8ca1f0755594aa28.png) , correto?
, correto?