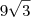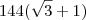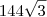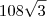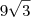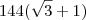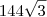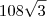por rochadapesada » Qui Abr 11, 2013 18:15
por rochadapesada » Qui Abr 11, 2013 18:15
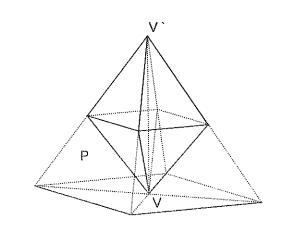
Considere um octaedro regular, cuja a aresta mede 6 cm e um de seus vértices V repousa sobre um plano P perpendicular ao eixo que contém V (ver figura). Prolongando-se as quatro arestas que partem do outro vértice V', que está na perpendicular a P em V, até interceptar o plano P, forma-se uma pirâmide regular de base quadrangular.
Assinale, então, dentre as alternativas a seguir, a única que corresponde à área total dessa pirâmide assim construída.
a)
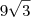

b)


c)
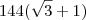

d)
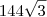

e)
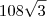

Eu Não consigo desenvolver ela, não sei por onde começar, o que fazer =s
- Anexos
-
- Sem títulao.png (16.06 KiB) Exibido 6274 vezes
-
rochadapesada
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Abr 04, 2013 22:00
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por young_jedi » Sáb Abr 13, 2013 22:13
por young_jedi » Sáb Abr 13, 2013 22:13
o octaedro pode ser decomposto em duas piramedes identicas sendo uma delas de cabeça pra baixo, prolongando os seguimentos obtemos uma piramede proporcioal a essas duas piramedes sendo que sua altura é o dobro das outras duas então pela relação de proporção temos que seus lados medem o dobro dos lados do octaedro ou seja 12, sendo assim é so calcular a area das faces, sendo que são quatro triangulos equilateros e um quadrado todos de lado 12
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por rochadapesada » Dom Abr 14, 2013 17:33
por rochadapesada » Dom Abr 14, 2013 17:33
Brigadão cara, na moral Obrigado msm =D
-
rochadapesada
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Abr 04, 2013 22:00
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Geometria Espacial
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Circunscrição de sólidos] Esfera e octaedro regular
por adlehs » Qui Nov 12, 2015 03:01
- 2 Respostas
- 4517 Exibições
- Última mensagem por adauto martins

Sáb Nov 14, 2015 15:00
Geometria Espacial
-
- [Geometria Espacial] Questão sobre Prisma Hexagonal Regular
por passolarg0f » Qui Abr 19, 2012 21:42
- 0 Respostas
- 2626 Exibições
- Última mensagem por passolarg0f

Qui Abr 19, 2012 21:42
Geometria Espacial
-
- Geometria Analítica - Polígono regular
por fyensinomedio » Sex Nov 08, 2013 13:04
- 1 Respostas
- 2825 Exibições
- Última mensagem por e8group

Sex Nov 08, 2013 20:38
Geometria Analítica
-
- [Geometria Plana] Polígono Regular
por edinaldoprof » Seg Fev 13, 2017 14:08
- 0 Respostas
- 2394 Exibições
- Última mensagem por edinaldoprof

Seg Fev 13, 2017 14:08
Geometria Plana
-
- geometria espacial
por Gir » Seg Jul 27, 2009 11:46
- 3 Respostas
- 11733 Exibições
- Última mensagem por Molina

Ter Jul 28, 2009 15:21
Problemas do Cotidiano
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.