Seja
 um valor fixado no intervalo
um valor fixado no intervalo ![\left[0,\frac{\pi}{2} \right] \left[0,\frac{\pi}{2} \right]](/latexrender/pictures/1383a7ee0ed99beee339c92e7a5fae08.png) . Sabe-se que a1=cotg
. Sabe-se que a1=cotg  é o primeiro termo de uma PG infinita de razão q =
é o primeiro termo de uma PG infinita de razão q =  .A soma de todos os termos dessa progressão é :
.A soma de todos os termos dessa progressão é :gabarito : sec
 .cossec
.cossec 

 um valor fixado no intervalo
um valor fixado no intervalo ![\left[0,\frac{\pi}{2} \right] \left[0,\frac{\pi}{2} \right]](/latexrender/pictures/1383a7ee0ed99beee339c92e7a5fae08.png) . Sabe-se que a1=cotg
. Sabe-se que a1=cotg  é o primeiro termo de uma PG infinita de razão q =
é o primeiro termo de uma PG infinita de razão q =  .A soma de todos os termos dessa progressão é :
.A soma de todos os termos dessa progressão é : .cossec
.cossec 

 .
.  .
. .
. 
 .
.  em ambos membros , temos
em ambos membros , temos  .
.  ; desde que
; desde que  ,ou seja ,
,ou seja ,  . Podemos ,multiplicar ambos membros por
. Podemos ,multiplicar ambos membros por  obtendo ,
obtendo ,  .
.  :
:  e
e  ,temos então que obrigatoriamente
,temos então que obrigatoriamente  e
e  .
.  é um valor fixado no intervalo
é um valor fixado no intervalo  e não
e não ![\left[0,\pi/2\right] \left[0,\pi/2\right]](/latexrender/pictures/4bb510c32589d41db3084fd07db1dcfd.png) .Com estas condições podemos aplicar a fórmula
.Com estas condições podemos aplicar a fórmula  ,segue
,segue  que devido a
que devido a 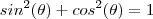 ,
,  .
.
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes