 por Jhennyfer » Ter Abr 09, 2013 14:03
por Jhennyfer » Ter Abr 09, 2013 14:03
Dois ângulos complementares A e B, sendo A < B, têm medidas na razão de 13 para17. consequentemente, a razão da medida do suplemento do ângulo A para o suplemento do ângulo B vale:
a) 43/47 b)17/13 c)13/17 d)119/48 e)47/43
-
Jhennyfer
- Usuário Parceiro

-
- Mensagens: 67
- Registrado em: Sáb Mar 30, 2013 15:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Ter Abr 09, 2013 19:43
por e8group » Ter Abr 09, 2013 19:43
Pelo encunciado temos que :
(a)
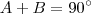
(b)
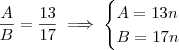
para algum

.
(c) Tal número

é 3 ,pois (a)+(b)
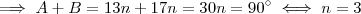
.
(d) O suplemento dos ângulos

e

são ,respectivamente ,
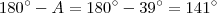
e
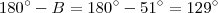
(e) Conclusão :
... complete você .
Tente concluir .
Deve encontar 47/43 .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Jhennyfer » Ter Abr 09, 2013 20:25
por Jhennyfer » Ter Abr 09, 2013 20:25
Consegui compreender...
Me confundi na parte inicial, por isso não consegui desenvolver o calculo...
Neste outro caso... uso a mesma linha de raciocinio? Estou resolvendo, e está dando uma conta enorme.
(CEFET-CE) Dois ângulos são suplementares. Os 2/3 do maior excedem os 3/4 do menor em 69º. Determine os ângulos:
-
Jhennyfer
- Usuário Parceiro

-
- Mensagens: 67
- Registrado em: Sáb Mar 30, 2013 15:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Ter Abr 09, 2013 20:50
por e8group » Ter Abr 09, 2013 20:50
OK.Só uma observação ,post uma única dúvida por tópico ,certo ?
Então , vamos impor que

e

são ângulos com
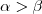
e
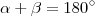
. Pelo enunciado "... Os 2/3 do maior excedem os 3/4 do menor em 69º ..." ,nesta parte diz que
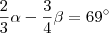
.
Em resumo temos um sistema de duas equações para duas incógnitas ,precisamos encontrar

e

tais que satisfaçam cada equação do sistema
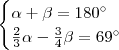
.
Consegue concluir ?
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Jhennyfer » Qui Abr 11, 2013 00:52
por Jhennyfer » Qui Abr 11, 2013 00:52
Ok, eu sei dessa regra e esqueci, desculpa (rs...)
Enfim... Na minha solução 36º e 144º... correto?
-
Jhennyfer
- Usuário Parceiro

-
- Mensagens: 67
- Registrado em: Sáb Mar 30, 2013 15:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Qui Abr 11, 2013 12:35
por e8group » Qui Abr 11, 2013 12:35
Se
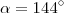
e
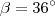
satisfazerem as duas equações ,então sua resposta está correta .
Verificando :
(1)
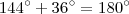
(OK !!)
(2)
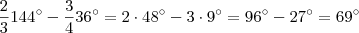
(OK!!) .
Está correto a sua resposta .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



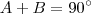
 para algum
para algum  .
.  é 3 ,pois (a)+(b)
é 3 ,pois (a)+(b) 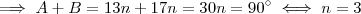 .
. e
e  são ,respectivamente ,
são ,respectivamente , 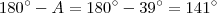 e
e 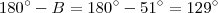


 e
e  são ângulos com
são ângulos com 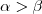 e
e 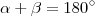 . Pelo enunciado "... Os 2/3 do maior excedem os 3/4 do menor em 69º ..." ,nesta parte diz que
. Pelo enunciado "... Os 2/3 do maior excedem os 3/4 do menor em 69º ..." ,nesta parte diz que 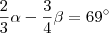 .
.  e
e  tais que satisfaçam cada equação do sistema
tais que satisfaçam cada equação do sistema 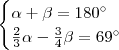 .
.

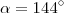 e
e 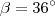 satisfazerem as duas equações ,então sua resposta está correta .
satisfazerem as duas equações ,então sua resposta está correta . 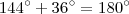 (OK !!)
(OK !!)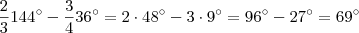 (OK!!) .
(OK!!) .





