Decomponha uî = (1,2,4) como soma de um vetor paralelo à reta r: X = (1,9,18) + ?(2,1,0) com outro paralelo ao plano
?:
x= 1 + ?
y = 1+ µ
z = ? - µ
Já tentei fazer de todas as formas que conheço mas não resultaram na resposta: uî = (11,7,4) + (-10,-5,0).


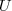 pode ser escrito como combinação linear de
pode ser escrito como combinação linear de  e
e  ,isto é ,
,isto é ,  .Onde os vetores
.Onde os vetores 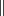 ao vetor diretor da reta .Já em relação ao plano , se os pontos A,B pertencem a um mesmo plano então o vetor
ao vetor diretor da reta .Já em relação ao plano , se os pontos A,B pertencem a um mesmo plano então o vetor  é paralelo a este plano .Ora ,se estamos procurando um vetor que é paralelo a este plano ,concluímos então que este vetor é múltiplo escalar de
é paralelo a este plano .Ora ,se estamos procurando um vetor que é paralelo a este plano ,concluímos então que este vetor é múltiplo escalar de 
