rochadapesada,
bom dia!
É uma questão bem trabalhosa!

Vou deixar as dicas, mas, caso não consiga retorne com as dúvidas e resolvemos juntos, ok?!
Ahhh! Não é tão trabalhosa como pensei, pois o intervalo não é dos maiores.
Segue a resolução:
Múltiplos de 6 naquele intervalo: {6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, 78, 84, 90, 96};
Múltiplos de 8 naquele intervalo: {8, 16,
24, 32, 40,
48, 56, 64,
72, 80, 88,
96};
Apliquemos uma P.A para saber a soma dos termos acima.
Múltiplos de 6:
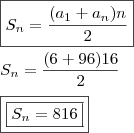
Múltiplos de 8:
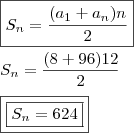
Aos múltiplos de 8, devemos subtrair aqueles que são comuns aos múltiplos de 6; e eles também formam uma P.A, por isso:
Múltiplos de

:
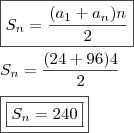
Portanto, a soma dos múltiplos de 6 e de 8 é:

Encontremos agora a soma TOTAL do intervalo, que também forma uma P.A, daí:

Por fim, a soma daqueles que não são múltiplos de 6 é dada pela subtração entre o TOTAL e os múltiplos de 6 e 8.
Com efeito,




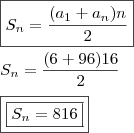
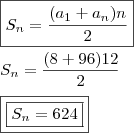
 :
: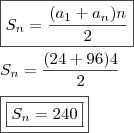






 .
.
 :
: