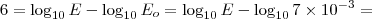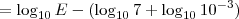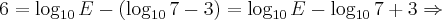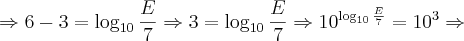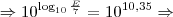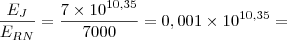por Anastacia Vaz » Dom Abr 07, 2013 12:03
por Anastacia Vaz » Dom Abr 07, 2013 12:03
Gostaria de ajuda para resolver a seguinte questão:
No ano de 1986, o município de João Câmara – RN foi atingido por uma sequência de tremores sísmicos, todos com magnitude maior do que ou igual a 4,0 na escala Richter. Tal escala segue a fórmula empírica, em que M é a magnitude, E é a energia liberada em KWh e E0=7x10-3KWh.
Recentemente, em março de 2011, o Japão foi atingido por uma inundação provocada por um terremoto. A magnitude desse terremoto foi de 8,9 na escala Richter. Considerando um terremoto de João Câmara com magnitude 4,0, pode-se dizer que a energia liberada no terremoto do Japão foi
A) 107,35 vezes maior do que a do terremoto de João Câmara.
B) cerca de duas vezes maior do que a do terremoto de João Câmara.
C) cerca de três vezes maior do que a do terremoto de João Câmara.
D) 1013,35 vezes maior do que a do terremoto de João Câmara.
Resposta Gabarito: A
-
Anastacia Vaz
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sáb Abr 06, 2013 17:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Comunicação
- Andamento: formado
 por nakagumahissao » Dom Abr 14, 2013 13:45
por nakagumahissao » Dom Abr 14, 2013 13:45
Por favor, utilize o editor de equações quando for postar. Aprender a utilizá-lo não vai lhe tomar mais que alguns minutos.
Ficaram faltando as equações (fórmulas) na postagem da sua questão, que deveria ter sido a seguinte:
No ano de 1986, o município de João Câmara – RN foi atingido por uma sequência de tremores sísmicos, todos com magnitude maior do que ou igual a 4,0 na escala Richter. Tal escala segue a fórmula empírica

, em que M é a magnitude, E é a energia liberada em KWh e E0 = 7 x 10-3 KWh. Recentemente, em março de 2011, o Japão foi atingido por uma inundação provocada por um terremoto. A magnitude desse terremoto foi de 8,9 na escala Richter. Considerando um terremoto de João Câmara com magnitude 4,0, pode-se dizer que a energia liberada no terremoto do Japão foi:
a)

vezes maior do que a do terremoto de João Câmara.
b) cerca de duas vezes maior do que a do terremoto de João Câmara.
c) cerca de três vezes maior do que a do terremoto de João Câmara.
d)

vezes maior do que a do terremoto de João Câmara.
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
 por nakagumahissao » Dom Abr 14, 2013 14:34
por nakagumahissao » Dom Abr 14, 2013 14:34
RESOLUÇÃO:
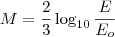
Em João Câmara - RN, foi constatado 4,0 nesta escala. Logo:

,
Mas,
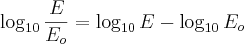
.
Então:
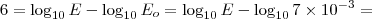
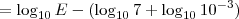
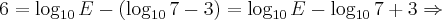
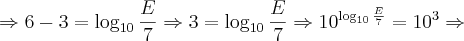

Façamos, de forma semelhante, para o terremoto do Japão, cuja magnitude foi de 8,9:
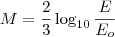




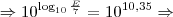

Como estamos querendo comparar as duas energias, devemos então dividir os resultados para E entre Japão e de João Câmara - RN para termos a proporção. Então:
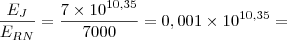

Logo:
O terremoto do Japão foi 10^7,35 vezes maior que o de João Câmara e a resposta correta é (a).
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Probabilidade - Questão 57 do Vestibular UESB 2012
por Janffs » Qui Nov 15, 2012 16:26
- 4 Respostas
- 10538 Exibições
- Última mensagem por young_jedi

Sex Mar 30, 2018 12:38
Probabilidade
-
- [Função modular] Vestibular da UEPB 2012
por rickminick » Ter Jul 10, 2012 13:17
- 2 Respostas
- 8717 Exibições
- Última mensagem por rickminick

Seg Jul 16, 2012 01:33
Funções
-
- Questão CEFET-MG 2012
por Thulio_Parazi » Qui Abr 05, 2012 13:48
- 5 Respostas
- 4813 Exibições
- Última mensagem por fraol

Ter Abr 10, 2012 20:02
Trigonometria
-
- Cefet-mg 2012 questão 03
por Thulio_Parazi » Sex Abr 13, 2012 11:12
- 4 Respostas
- 4482 Exibições
- Última mensagem por fraol

Qua Abr 18, 2012 22:26
Logaritmos
-
- questão 69 da Fuvest 2012
por Alane » Dom Ago 05, 2012 13:03
- 4 Respostas
- 11735 Exibições
- Última mensagem por Nina Luizet

Dom Ago 02, 2015 15:31
Probabilidade
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 , em que M é a magnitude, E é a energia liberada em KWh e E0 = 7 x 10-3 KWh. Recentemente, em março de 2011, o Japão foi atingido por uma inundação provocada por um terremoto. A magnitude desse terremoto foi de 8,9 na escala Richter. Considerando um terremoto de João Câmara com magnitude 4,0, pode-se dizer que a energia liberada no terremoto do Japão foi:
, em que M é a magnitude, E é a energia liberada em KWh e E0 = 7 x 10-3 KWh. Recentemente, em março de 2011, o Japão foi atingido por uma inundação provocada por um terremoto. A magnitude desse terremoto foi de 8,9 na escala Richter. Considerando um terremoto de João Câmara com magnitude 4,0, pode-se dizer que a energia liberada no terremoto do Japão foi: vezes maior do que a do terremoto de João Câmara.
vezes maior do que a do terremoto de João Câmara. vezes maior do que a do terremoto de João Câmara.
vezes maior do que a do terremoto de João Câmara.
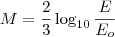
 ,
,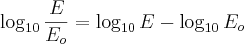 .
.