 por KleinIll » Sex Abr 05, 2013 12:56
por KleinIll » Sex Abr 05, 2013 12:56
Calcule
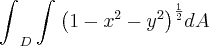
, onde D é o disco

, identificando primeiro a integral como o volume de um sólido.
??? ?? ? ????, ? ? ??????.
-

KleinIll
- Usuário Dedicado

-
- Mensagens: 46
- Registrado em: Qua Out 31, 2012 14:17
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Química
- Andamento: formado
 por Russman » Sex Abr 05, 2013 21:00
por Russman » Sex Abr 05, 2013 21:00
O 1° passo é verificar se há simetria no problema. Se sim, qual? Você sabe dizer?
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por KleinIll » Sáb Abr 06, 2013 00:47
por KleinIll » Sáb Abr 06, 2013 00:47
Não. Esta é uma questão retirada do livro James Stewart Volume 2.
Edição: Não é necessário responder este tópico mais pois eu já consegui esclarecer minha dúvida. Depois de converter para coordenadas polares eu consegui integrar.
Russman, desculpa se eu estiver ofendendo, mas eu acho mais do que justo deixar claro que quando alguém pede ajuda aqui é porque não sabe fazer a conta/questão, então, ao invés responder com outra pergunta, responda a resolução. Novamente, desculpa se eu estou ofendendo.
??? ?? ? ????, ? ? ??????.
-

KleinIll
- Usuário Dedicado

-
- Mensagens: 46
- Registrado em: Qua Out 31, 2012 14:17
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Química
- Andamento: formado
 por Russman » Sáb Abr 06, 2013 16:21
por Russman » Sáb Abr 06, 2013 16:21
KleinIll escreveu:Russman, desculpa se eu estiver ofendendo, mas eu acho mais do que justo deixar claro que quando alguém pede ajuda aqui é porque não sabe fazer a conta/questão, então, ao invés responder com outra pergunta, responda a resolução. Novamente, desculpa se eu estou ofendendo.
Não ofendeu. Esse seu pensamento, que é lastimável, é muito comum. Se eu tivesse lhe resolvido a questão, isto é, tivesse lhe entregue a resolução, eu NÃO estaria lhe ajudando. Ajudar a resolver questões matemáticas é encaminhar um raciocínio que o guiará até a solução completa por si mesmo. Quem deve ser capaz de solucionar o problema é VOCÊ, e não eu, pois eu já sei. Afinal, se você sabe resolver somente este exercício(ou uma meia dúzia semelhante) você não sabe coisa alguma sobre integrais duplas.
KleinIll escreveu:Depois de converter para coordenadas polares eu consegui integrar.
A isto que eu me referia. O problema tem simetria polar. Assim, convertendo para o sistema polar de coordenadas o problema pode ser resolvido facilmente. Era esse o 1° passo.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por KleinIll » Sáb Abr 06, 2013 18:18
por KleinIll » Sáb Abr 06, 2013 18:18
Concordo com você, sou eu quem precisa aprender e entendo que você queira primeiramente saber qual é minha dúvida especificadamente. Tudo bem, eu posso estar "errado" por pedir a resolução, mas eu tenho a consciência e a capacidade de distinguir o que é a minha dúvida e o que é um "tipo" de exercício. Inclusive quando eu posto alguma dúvida aqui, no site, eu adiciono o máximo de comentários possíveis. Nesta questão eu não tive este cuidado pois preferi ver a resolução completa. De qualquer forma, obrigado pela atenção e compreensão.
??? ?? ? ????, ? ? ??????.
-

KleinIll
- Usuário Dedicado

-
- Mensagens: 46
- Registrado em: Qua Out 31, 2012 14:17
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Química
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integral Tripla (Resolvida)] Volume de Sólido
por raimundoocjr » Seg Dez 16, 2013 23:33
- 1 Respostas
- 3783 Exibições
- Última mensagem por young_jedi

Ter Dez 17, 2013 19:48
Cálculo: Limites, Derivadas e Integrais
-
- [Volume] Integral dupla
por Claudio Parana » Qua Fev 05, 2014 21:33
- 1 Respostas
- 2413 Exibições
- Última mensagem por young_jedi

Seg Fev 17, 2014 21:27
Cálculo: Limites, Derivadas e Integrais
-
- Calculo de volume atravé de integral dupla
 por maiquel » Qua Out 13, 2010 12:34
por maiquel » Qua Out 13, 2010 12:34
- 1 Respostas
- 7392 Exibições
- Última mensagem por armando

Sex Jan 06, 2017 04:14
Cálculo: Limites, Derivadas e Integrais
-
- [Coordenada Polar] Volume por Integral Dupla
por raimundoocjr » Qui Dez 12, 2013 19:42
- 0 Respostas
- 2404 Exibições
- Última mensagem por raimundoocjr

Qui Dez 12, 2013 19:42
Cálculo: Limites, Derivadas e Integrais
-
- Volume do Solido
por leha » Qui Dez 10, 2009 10:22
- 3 Respostas
- 3385 Exibições
- Última mensagem por leha

Seg Dez 14, 2009 13:44
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
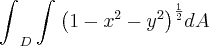 , onde D é o disco
, onde D é o disco  , identificando primeiro a integral como o volume de um sólido.
, identificando primeiro a integral como o volume de um sólido.
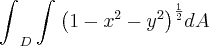 , onde D é o disco
, onde D é o disco  , identificando primeiro a integral como o volume de um sólido.
, identificando primeiro a integral como o volume de um sólido.




