Seja M um ponto que divide em duas partes iguais o arco AB de uma semi-circunferência, cujo diâmetro é
.Um raio de luz é emitido desde A e atinge a semi-circunferência num ponto Q entre M e B, e então é refletido, cruzando o diâmetro AB no ponto P.
Obtenha o valor limite do comprimento do segmento AP quando o ponto Q se aproxima infinitamente do ponto B.
Minha resolução:
[Res.] Sendo O o centro da circunferência, sei que OP=
e ângulo OAQ= ângulo AQO= ângulo OQP.Aplicando o teorema do seno no triângulo OQP e sabendo que , ângulo POQ= 2*(ângulo OAQ) e ângulo OPQ= pi-3*(ângulo OAQ), tenho que:
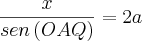
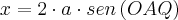
AP=
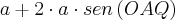
Portanto,
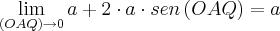
Correto ou errado?
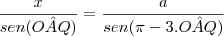
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")