O limite para o ponto de coordenada x=-7 é encontrado fazendo a substituição de x por -7.
Mas isso é permitido pelo motivo que em geral toda função fracionária só possui um valor limite (valor finito), quando o limite da função do numerador desta função fracionária, seja igual a 0, e o limite da função do denominador desta função fracionária também seja igual a zero. Caso o limite da função do numerador e/ou denominador desta função fracionária seja diferente de zero, então pode haver dois tipos de resultados:
1)
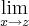

=0 em que b é diferente de zero e z é qualquer valor real.
2)
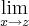

=
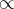
em que b é diferente de zero e z é qualquer valor real.
Observe que a divisão por zero é indefinida, somente o limite da divisão de um valor diferente de zero por uma valor igual a zero, é que é igual ao infinito.
Resumindo: o valor do limite da sua função fracionária quando x se aproxima de -7 é o infinito, e por ser o infinito um valor não real, tal limite é indefinido ou inexistente no campo do corpo dos números reais.



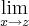
 =0 em que b é diferente de zero e z é qualquer valor real.
=0 em que b é diferente de zero e z é qualquer valor real.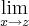
 =
=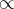 em que b é diferente de zero e z é qualquer valor real.
em que b é diferente de zero e z é qualquer valor real.


 , avisa que eu resolvo.
, avisa que eu resolvo.

