


 . Eles não são semelhantes!
. Eles não são semelhantes!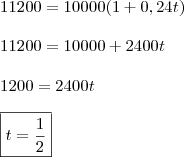












Cleyson007 escreveu:Amigo danjr5, se me permite uma vez que estou online..(...)
Tay escreveu:Eu percebi que se eu não simplificar 1200/2400 , o que creio eu não ser errado, obterei 0,5. Ah, sim, neste caso, simplificar facilita a vida porque dá a resposta diretamente. Porque eu refiz aqui e dividindo 1200/2400 dá como resultado 0,5 ; Entretanto, eu terei que multiplicá-lo por 12 (ano) pra achar 6. Humm. Tenho dificuldade pra encontrar resultados em meses, dias.. Quando eu me enroscar com um exercícios desses, voltarei a pedir ajudar, hein. . ?! rs
 também será em anos.
também será em anos.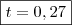 . Veja:
. Veja:







24 (meses) não dá para dividir por 100, então, transformei os meses em dias. Para isso, multipliquei 24 por 30, afinal, um mês tem trinta dias;

 resposta às suas dúvidas, no entanto, elas se perderam graças a uma falha em minha conexão e, não consegui recuperá-las. E, por hoje, não disponho do tempo inicial; por essa razão, se houver alguma dúvida, não exite em perguntar, ok?!
resposta às suas dúvidas, no entanto, elas se perderam graças a uma falha em minha conexão e, não consegui recuperá-las. E, por hoje, não disponho do tempo inicial; por essa razão, se houver alguma dúvida, não exite em perguntar, ok?!Tay escreveu:Boa noite,
Infelizmente, ainda não compreendi tudo, por exemplo,
- porque você dividiu 0,27 por 100, porque 100?
 .
.Tay escreveu: - depois, se eu tivesse nesse caminho, dividiria o 324/100 e obteria 3,24 deduzindo que fossem 3 anos e 24 dias ou meses (dias no caso já que se fossem meses não seriam mais 3, e sim, 5 anos, né??, rs).
Tay escreveu: - Quando você diz que não é possível dividir 24 por 100 é porque o resultado será uma dízima?
Tay escreveu: -Além disso, 24 não poderia, em outra situação, por exemplo, serem dias, sempre acontecerá de serem meses, conforme aconteceu aqui?
Tay escreveu: - E o 'passo a passo' será sempre esse, transformar do maior - anos para meses, meses para dias, dias para horas - para o menor, e sempre poderei utilizar o método que você está me explicando?
Tay escreveu: Quantas perguntas, espero que eu tenha conseguido expressar minhas dúvidas, muito obrigada.
Tay





Voltar para Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes


 , avisa que eu resolvo.
, avisa que eu resolvo.

