 por marcosmuscul » Ter Mar 26, 2013 12:52
por marcosmuscul » Ter Mar 26, 2013 12:52
segue abaixo a expressão.
Amigos, já tentei de todo jeito que eu pude mas não consigo sair desta situação. Se alguém puder me ajudar eu agradeço.
- Anexos
-
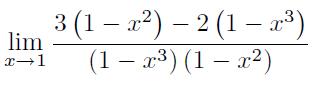
- esta é a expressão
- limite.JPG (5.34 KiB) Exibido 1975 vezes
-
marcosmuscul
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Ter Mar 19, 2013 15:48
- Localização: RJ
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: a começar engenharia civil
- Andamento: cursando
 por Russman » Ter Mar 26, 2013 14:08
por Russman » Ter Mar 26, 2013 14:08
É só ir fatorando os termos.
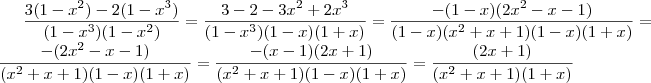
Agora para

não há problema. Você deve calcular

"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por marcosmuscul » Ter Mar 26, 2013 19:48
por marcosmuscul » Ter Mar 26, 2013 19:48
obrigado amigo. calculo esclarecedor.
-
marcosmuscul
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Ter Mar 19, 2013 15:48
- Localização: RJ
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: a começar engenharia civil
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- * Trigonometria : Questões simples que não consigo fazer!!!
por Thiago Valenca » Seg Abr 16, 2012 17:38
- 4 Respostas
- 2970 Exibições
- Última mensagem por DanielFerreira

Sáb Abr 21, 2012 17:47
Trigonometria
-
- consigo fazer tudo e sempre enrosco no final.
por ricardosanto » Ter Abr 17, 2012 22:34
- 1 Respostas
- 1598 Exibições
- Última mensagem por TheoFerraz

Ter Abr 17, 2012 23:42
Cálculo: Limites, Derivadas e Integrais
-
- [nao consigo fazer desde o inicio] nunca fiz sozinho só
por jeffinps » Ter Fev 26, 2013 14:47
- 4 Respostas
- 2969 Exibições
- Última mensagem por jeffinps

Qua Fev 27, 2013 15:21
Cálculo: Limites, Derivadas e Integrais
-
- [limite] Cancelar denominador
por emanes » Sex Ago 17, 2012 09:34
- 1 Respostas
- 1724 Exibições
- Última mensagem por e8group

Sex Ago 17, 2012 10:22
Cálculo: Limites, Derivadas e Integrais
-
- Limite com raiz de X no denominador
por janainasabidussi » Dom Out 26, 2014 17:42
- 1 Respostas
- 2187 Exibições
- Última mensagem por adauto martins

Seg Out 27, 2014 14:14
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



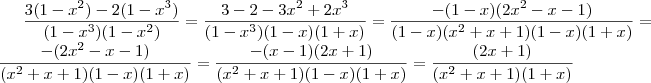
 não há problema. Você deve calcular
não há problema. Você deve calcular 



 .
.



