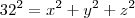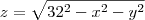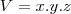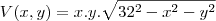por caiormagno » Dom Mar 24, 2013 22:04
por caiormagno » Dom Mar 24, 2013 22:04
Galera. To com umas questões pra levar pra prova amanhã. Tem como me ajudar?
1) O comprimento da diagonal de uma caixa retangular deve ser 32. Qual é o maior volume?
2) Deduzir as formulas aproximadas de até os termos de ordem (a:1 e letra b:2) para a função arctang ((1+a)/1-b).
3) Aplicando a formula de taylor, até ordem a) 1; b)2 calcular aproximadamente (0,95)elevado a 2,01.
use função z = x elevado a y = exp (ylnx) em ponto (1,1))
Qualquer uma ja ajuda galera. Obrigado
-
caiormagno
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Dom Mar 24, 2013 21:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia de produção
- Andamento: cursando
 por young_jedi » Ter Mar 26, 2013 13:07
por young_jedi » Ter Mar 26, 2013 13:07
supondo a caixa com lados x,y e z
temos que
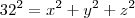
então
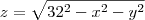
o volume é igual a
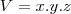
então
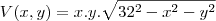
calcule as derivada parciais com relação a x e y e iguale a 0 então encontre x e y e depois z
comente ai qualquer coisa
as outras duas quetões não entendi muito bem, se aparecer qualquer ideia eu posto aqui
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [limite] Help com urgencia
por gaaby » Qui Jun 14, 2012 15:33
- 2 Respostas
- 1568 Exibições
- Última mensagem por gaaby

Qui Jun 14, 2012 15:53
Cálculo: Limites, Derivadas e Integrais
-
- Preciso de ajuda com urgência..
por Nogueira01 » Qui Ago 06, 2015 10:31
- 2 Respostas
- 4772 Exibições
- Última mensagem por Nogueira01

Sex Ago 07, 2015 08:31
Matemática Financeira
-
- [DESAFIO DE PROBABILIDADE] Tempo de espera na urgência
por PTuga » Sáb Out 26, 2013 18:11
- 0 Respostas
- 1240 Exibições
- Última mensagem por PTuga

Sáb Out 26, 2013 18:11
Probabilidade
-
- Prova de Cálculo Usp
por ARCS » Seg Fev 28, 2011 00:46
- 0 Respostas
- 2551 Exibições
- Última mensagem por ARCS

Seg Fev 28, 2011 00:46
Pedidos de Materiais
-
- [Logaritmo] duas questões para resolução com urgência
por Cristian Cristiano » Qua Mai 03, 2017 04:37
- 0 Respostas
- 4054 Exibições
- Última mensagem por Cristian Cristiano

Qua Mai 03, 2017 04:37
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 11 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.