![s(t)=m/c*ln cos h*\sqrt[2]{gc/mt} s(t)=m/c*ln cos h*\sqrt[2]{gc/mt}](/latexrender/pictures/a2351c9b573bd7633040cde4be4133c8.png) , em que c é uma constante positiva. Encontre
, em que c é uma constante positiva. Encontre  .
. Primeiro da ?*0, ai eu inverti o c e ficou m*c no começo da formula, mas nao to conseguindo resolver. Alguem pode dar uma ajuda?

![s(t)=m/c*ln cos h*\sqrt[2]{gc/mt} s(t)=m/c*ln cos h*\sqrt[2]{gc/mt}](/latexrender/pictures/a2351c9b573bd7633040cde4be4133c8.png) , em que c é uma constante positiva. Encontre
, em que c é uma constante positiva. Encontre  .
. 
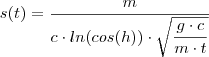 ou (2)
ou (2) 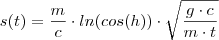 .Outra pergunta : Não seria para calcular
.Outra pergunta : Não seria para calcular  ao invés de
ao invés de  .Por favor ,confirme estas informações
.Por favor ,confirme estas informações

 é constante positiva ,isto é ,
é constante positiva ,isto é , é fixo . Desta forma, não faz sentido
é fixo . Desta forma, não faz sentido 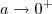 podemos sim ter
podemos sim ter  pequeno o quanto queremos, neste caso ,
pequeno o quanto queremos, neste caso , .Em consequência, não podemos afirmar nada sobre o comportamento de
.Em consequência, não podemos afirmar nada sobre o comportamento de 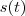 para qualquer
para qualquer  e sim à medida que
e sim à medida que  percorre
percorre  ,pois ,
,pois ,  não é uma função constante e nem limitada .
não é uma função constante e nem limitada . 


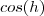 e sim cosseno hiperbólico .Neste contexto ,
e sim cosseno hiperbólico .Neste contexto , ![s(t) = \frac{m}{c} ln\left[cosh\left( \sqrt{\frac{g\cdot c}{m\cdot t}}\right ) \right ] = \frac{g}{u^2 \cdot t} \cdot ln\left[\frac{e^{u} + e^{-u}}{2} \right ] s(t) = \frac{m}{c} ln\left[cosh\left( \sqrt{\frac{g\cdot c}{m\cdot t}}\right ) \right ] = \frac{g}{u^2 \cdot t} \cdot ln\left[\frac{e^{u} + e^{-u}}{2} \right ]](/latexrender/pictures/5a12edfc56319a898f8670668cd345b9.png) ,onde estamos considerando
,onde estamos considerando 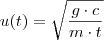 .
.  . Assim ,
. Assim , ![\lim_{c\to0^+} s(t) = \lim_{u\to0^+}\frac{g}{u^2 \cdot t} \cdot ln\left[\frac{e^{u} + e^{-u}}{2} \right ] = \lim_{u\to0^+} \frac{g}{t} \cdot \frac{ln\dfrac{e^u + e^{-u}}{2}}{u^2} \lim_{c\to0^+} s(t) = \lim_{u\to0^+}\frac{g}{u^2 \cdot t} \cdot ln\left[\frac{e^{u} + e^{-u}}{2} \right ] = \lim_{u\to0^+} \frac{g}{t} \cdot \frac{ln\dfrac{e^u + e^{-u}}{2}}{u^2}](/latexrender/pictures/25ebf67edf64bd38db5b193ed23b7dec.png) .
. 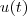 e fazendo as devidas simplificações ,vamos obter o seguinte limite equivalente ,
e fazendo as devidas simplificações ,vamos obter o seguinte limite equivalente , 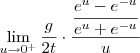 que por sua vez também apresenta indeterminação "0/0" ,portanto ,novamente por L'hospital ,segue que
que por sua vez também apresenta indeterminação "0/0" ,portanto ,novamente por L'hospital ,segue que![\lim_{u\to 0^+} \frac{g}{2t}\left[(e^u + e^{-u})^2 - (e^u - e^{-u})^2\right ] \lim_{u\to 0^+} \frac{g}{2t}\left[(e^u + e^{-u})^2 - (e^u - e^{-u})^2\right ]](/latexrender/pictures/6cd2eec21e2df32c3e849ceabbfe9272.png) .
.  e
e 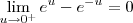 ,concluímos que
,concluímos que  .
.
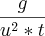 é pq vc inverteu o C, ficando m*c e depois multiplicou pela derivada da raiz ali? obrigado desde já
é pq vc inverteu o C, ficando m*c e depois multiplicou pela derivada da raiz ali? obrigado desde já
 ,certo ?
,certo ? 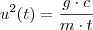 ,isolando
,isolando  ,obtemos
,obtemos 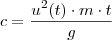 .Substituindo-se
.Substituindo-se  em
em  ,ficamos com
,ficamos com  ou
ou 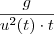 .
.
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes

 .
.



