 por kdeyse » Qua Mar 20, 2013 22:12
por kdeyse » Qua Mar 20, 2013 22:12
A media aritmatica das alturas de 5 edificios é de 85m. Se for acrescentado a apenas um dos edificios mais um andar de 3m de altura, a media entre eles passra a ser:
bom, eu iniciei assim :
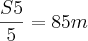
logo S5=425m
mas ai entao entra a duvida, nao sei como fazer para acresecntar esses 3m em apenas um dos edificios.. sera que podem me ajudar?
-
kdeyse
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Ter Jan 22, 2013 01:53
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Russman » Qua Mar 20, 2013 22:49
por Russman » Qua Mar 20, 2013 22:49
A média aritmética dos valores

é

tal que

.
A media aritmatica das alturas de 5 edificios é dada por
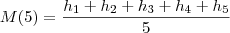
e este valor é dado no problema.
Agora suponha que você adicione 3 m de altura no edificio

. Então,
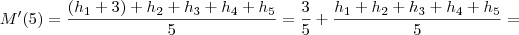
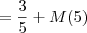
.
Como você sabe o valor de

basta substituir e calcular

.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por kdeyse » Qui Mar 21, 2013 12:24
por kdeyse » Qui Mar 21, 2013 12:24
Obrigado...consegui resolver...da 85,6m né...
-
kdeyse
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Ter Jan 22, 2013 01:53
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Aritmética
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [equação 1º grau] Será que alguém pode me ajudar?
por patricia suede » Qua Mai 21, 2008 23:27
- 1 Respostas
- 1902 Exibições
- Última mensagem por admin

Qui Mai 22, 2008 02:13
Álgebra Elementar
-
- Alguem pode ajudar-me?
por carlos r m oliveira » Seg Out 05, 2009 11:35
- 1 Respostas
- 2539 Exibições
- Última mensagem por Neperiano

Dom Jul 03, 2011 21:05
Estatística
-
- Alguém pode me ajudar?
por apoliveirarj » Seg Jul 19, 2010 18:20
- 1 Respostas
- 3390 Exibições
- Última mensagem por Douglasm

Seg Jul 19, 2010 18:49
Matemática Financeira
-
- Alguém pode me ajudar?
por Andromeda » Seg Set 19, 2011 20:19
- 2 Respostas
- 2412 Exibições
- Última mensagem por Andromeda

Seg Set 19, 2011 21:13
Trigonometria
-
- lim x^2.sin(x/1), x=0. Alguém pode me ajudar?
por Arthur_Bulcao » Seg Abr 09, 2012 18:05
- 2 Respostas
- 2007 Exibições
- Última mensagem por fraol

Seg Abr 09, 2012 19:24
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
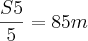 logo S5=425m
logo S5=425m 
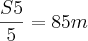 logo S5=425m
logo S5=425m 
 é
é  tal que
tal que  .
.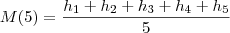
 . Então,
. Então,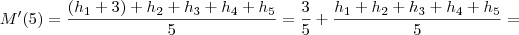
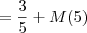 .
. basta substituir e calcular
basta substituir e calcular  .
.
