 por KleinIll » Qua Mar 20, 2013 16:32
por KleinIll » Qua Mar 20, 2013 16:32
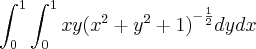
Derivando em y chego à:
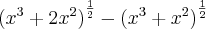
E apartir daí não consigo solução para a integral.
Como faz o cálculo desta integral dupla?
* Por favor, desconsidere o tópico, foi erro de conta e no lugar desta integral parcial em y, encontro a expressão x[(x² + 2)^(1/2) - (x² + 1)^(1/2)]
Editado pela última vez por
KleinIll em Qui Mar 21, 2013 09:05, em um total de 2 vezes.
??? ?? ? ????, ? ? ??????.
-

KleinIll
- Usuário Dedicado

-
- Mensagens: 46
- Registrado em: Qua Out 31, 2012 14:17
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Química
- Andamento: formado
 por Russman » Qua Mar 20, 2013 19:10
por Russman » Qua Mar 20, 2013 19:10
De onde vem essa expressão?
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por adauto martins » Dom Out 12, 2014 16:36
por adauto martins » Dom Out 12, 2014 16:36
![\int_{0}^{1}\int_{0}^{1}(xy)/\sqrt[2]{{x}^{2}+{y}^{2}+1}dxdy \int_{0}^{1}\int_{0}^{1}(xy)/\sqrt[2]{{x}^{2}+{y}^{2}+1}dxdy](/latexrender/pictures/8c022cc0ca50b45912c3ecdb406eb011.png)
,faz.x=rcosx,y=rsenx,teremos:
![\int_{0}^{1}\int_{0}^{1}(({r}^{2})(cos\theta)(sen\theta)\sqrt[2]{{rcosx}^{2}+{rsenx}^{2}+1})(-{r}^{2}((cos\theta)(sen\theta))drd\theta \int_{0}^{1}\int_{0}^{1}(({r}^{2})(cos\theta)(sen\theta)\sqrt[2]{{rcosx}^{2}+{rsenx}^{2}+1})(-{r}^{2}((cos\theta)(sen\theta))drd\theta](/latexrender/pictures/050fb78ff2d5d19cf8063c61db0c35ae.png)
![\int_{0}^{\pi/2}{-(cos\theta(sen\theta))}^{2}(\int_{0}^{1}({r}^{4}/(\sqrt[2]{{r}^{2}+1})dr)d\theta \int_{0}^{\pi/2}{-(cos\theta(sen\theta))}^{2}(\int_{0}^{1}({r}^{4}/(\sqrt[2]{{r}^{2}+1})dr)d\theta](/latexrender/pictures/e1be6ecb90d65197095cbbd389a92394.png)
...na integraçao em relaçao a r,faz-se u=
![\sqrt[2]{{r}^{2}+1} \sqrt[2]{{r}^{2}+1}](/latexrender/pictures/52c8355945ad48c489853577b99458d6.png)
e na segunda integraçao,em relaçao a

,faz-se v=sen

,levando-se em conta os limites de integraçao(0,1)...ai por substituiçao calcula-se a integral...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integral] integral dupla
por -civil- » Seg Abr 09, 2012 23:52
- 1 Respostas
- 1190 Exibições
- Última mensagem por LuizAquino

Ter Abr 10, 2012 11:18
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] integral dupla
por nalinelima » Sáb Out 13, 2012 21:54
- 1 Respostas
- 1117 Exibições
- Última mensagem por nalinelima

Sáb Out 13, 2012 21:55
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Integral Dupla
por RafaelPereira » Qui Jun 27, 2013 18:52
- 2 Respostas
- 1466 Exibições
- Última mensagem por RafaelPereira

Sex Jun 28, 2013 18:09
Cálculo: Limites, Derivadas e Integrais
-
- Integral dupla
por DanielFerreira » Sex Mar 16, 2012 23:56
- 2 Respostas
- 2867 Exibições
- Última mensagem por DanielFerreira

Sáb Mar 17, 2012 19:11
Cálculo: Limites, Derivadas e Integrais
-
- Integral dupla - 2
por DanielFerreira » Dom Mar 18, 2012 12:44
- 5 Respostas
- 4149 Exibições
- Última mensagem por DanielFerreira

Sex Mar 23, 2012 22:34
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
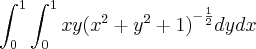
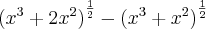



![\int_{0}^{1}\int_{0}^{1}(xy)/\sqrt[2]{{x}^{2}+{y}^{2}+1}dxdy \int_{0}^{1}\int_{0}^{1}(xy)/\sqrt[2]{{x}^{2}+{y}^{2}+1}dxdy](/latexrender/pictures/8c022cc0ca50b45912c3ecdb406eb011.png) ,faz.x=rcosx,y=rsenx,teremos:
,faz.x=rcosx,y=rsenx,teremos:![\int_{0}^{1}\int_{0}^{1}(({r}^{2})(cos\theta)(sen\theta)\sqrt[2]{{rcosx}^{2}+{rsenx}^{2}+1})(-{r}^{2}((cos\theta)(sen\theta))drd\theta \int_{0}^{1}\int_{0}^{1}(({r}^{2})(cos\theta)(sen\theta)\sqrt[2]{{rcosx}^{2}+{rsenx}^{2}+1})(-{r}^{2}((cos\theta)(sen\theta))drd\theta](/latexrender/pictures/050fb78ff2d5d19cf8063c61db0c35ae.png)
![\int_{0}^{\pi/2}{-(cos\theta(sen\theta))}^{2}(\int_{0}^{1}({r}^{4}/(\sqrt[2]{{r}^{2}+1})dr)d\theta \int_{0}^{\pi/2}{-(cos\theta(sen\theta))}^{2}(\int_{0}^{1}({r}^{4}/(\sqrt[2]{{r}^{2}+1})dr)d\theta](/latexrender/pictures/e1be6ecb90d65197095cbbd389a92394.png) ...na integraçao em relaçao a r,faz-se u=
...na integraçao em relaçao a r,faz-se u=![\sqrt[2]{{r}^{2}+1} \sqrt[2]{{r}^{2}+1}](/latexrender/pictures/52c8355945ad48c489853577b99458d6.png) e na segunda integraçao,em relaçao a
e na segunda integraçao,em relaçao a  ,faz-se v=sen
,faz-se v=sen .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
