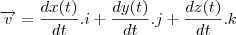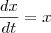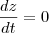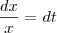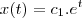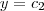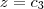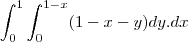por Piva » Qua Mar 20, 2013 10:36
por Piva » Qua Mar 20, 2013 10:36
Boa tarde,
Estou estudando cálculo vetorial atualmente, e me deparei com a seguinte questão que não consigo resolver de forma alguma. Será que alguém poderia me dar uma luz de como eu posso resolver, ou uma fonte de estudo que explique tal resolução? Meu professor não explicou Teorema de Stokes nem do Divergente ainda, dessa forma, não posso utiliza-los...
1)Resolva:
a) Seja o escoamento de um fluido compressível com campo de velocidades v = x i .
Mostre que as partículas individuais têm vetor de posição r ( t ) = c1 e^t i + c2 j + c3 k, com c1 , c2 , e c3 constantes. Mostre também que as partículas, que no instante t = 0 estão no cubo delimitado pelos
planos x = 0 , x = 1 , y = 0 , y = 1 , z = 0 , z = 1 ,ocupam no instante t = 1 o volume e.
b) Calcule a integral de superfície
?? F . dS para o campo vetorial F (x, y, z ) = xze y i - xze y j + z k sendo a superfície S orientada e definida como parte do plano x + y + z = 1 no primeiro octante, com orientação para baixo.
c) Um fluido de densidade 1500 flui com velocidade v = ? y i + x j + 2z k . Determine a taxa de vazão do fluido saindo da esfera x^2 + y^2 + z^2 = 25 .
Desde já, agradeço a colaboração..
Patrick
-
Piva
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qua Jun 29, 2011 18:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: cursando
 por young_jedi » Qua Mar 20, 2013 15:06
por young_jedi » Qua Mar 20, 2013 15:06
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Calculo Vetorial
por roger0196 » Seg Abr 04, 2011 15:02
- 6 Respostas
- 5364 Exibições
- Última mensagem por Jackie

Ter Abr 26, 2011 20:20
Geometria Analítica
-
- Calculo Vetorial
por Renato Lima » Qua Abr 27, 2011 22:21
- 1 Respostas
- 2081 Exibições
- Última mensagem por LuizAquino

Qua Abr 27, 2011 23:12
Geometria Analítica
-
- GA e Calculo Vetorial
por camposhj » Sex Out 07, 2011 00:41
- 3 Respostas
- 2457 Exibições
- Última mensagem por LuizAquino

Sex Out 07, 2011 13:06
Geometria Analítica
-
- Cálculo Vetorial
por Jhenrique » Ter Jul 02, 2013 19:10
- 0 Respostas
- 1587 Exibições
- Última mensagem por Jhenrique

Ter Jul 02, 2013 19:10
Cálculo: Limites, Derivadas e Integrais
-
- cálculo vetorial
por fasaatyro » Sáb Mai 02, 2015 12:02
- 0 Respostas
- 1276 Exibições
- Última mensagem por fasaatyro

Sáb Mai 02, 2015 12:02
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.