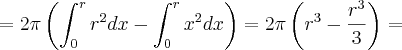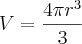por klueger » Ter Mar 19, 2013 13:58
por klueger » Ter Mar 19, 2013 13:58
Não sei deduzir esta fórmula... alguém pode ajudar?
O volume de um esfera de raio
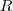
é dado por
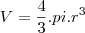
.
Com o estudo de integrais podemos provar que realmente esta fórmula do volume é verdadeira, basta pensar que uma esfera de raio R é gerada pela rotação em torno do eixo x da circunferência

.
Sendo assim usando os conceitos de volume de sólido de revolução
prove a fórmula do volume da esfera
-
klueger
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Dom Fev 03, 2013 15:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por e8group » Ter Mar 19, 2013 17:06
por e8group » Ter Mar 19, 2013 17:06
Solução :

.
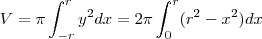
Tente concluir ...
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por nakagumahissao » Ter Mar 19, 2013 17:13
por nakagumahissao » Ter Mar 19, 2013 17:13
Resolução:
Demonstração:
Considere uma circunferência definida por:
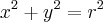
Considere ainda, que iremos 'rotacionar' em torno do eixo x apenas a parte do círculo situada no primeiro quadrante do gráfico, ou seja:
![y = \sqrt[]{r^{2} - x^{2}} y = \sqrt[]{r^{2} - x^{2}}](/latexrender/pictures/cd2d925abd7384eeabb03523959926e1.png)
e x =[0, r]
Como rotacionaremos apenas a parte do círculo do nosso primeiro quadrante, após termos calculado o volume da figura rotacionada no gráfico, teremos então que multiplicá-lo por 2 para termos o volume total. Desta maneira:
![V = 2\pi\int_{0}^{r} \left[\sqrt[]{r^{2} - x^{2}} \right]^{2} dx = 2\pi\int_{0}^{r} r^{2} - x^{2} dx = V = 2\pi\int_{0}^{r} \left[\sqrt[]{r^{2} - x^{2}} \right]^{2} dx = 2\pi\int_{0}^{r} r^{2} - x^{2} dx =](/latexrender/pictures/c0a479dc9f74960a3d32e3005ceb5b24.png)
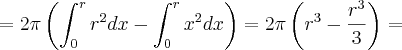

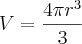
Como queríamos demonstrar.
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- O volume de uma esfera em relação a outra esfera
por Macedo Junior » Sáb Jul 23, 2016 21:01
- 2 Respostas
- 9568 Exibições
- Última mensagem por Macedo Junior

Sáb Jul 23, 2016 23:28
Geometria Plana
-
- Fórmula de volume de uma esfera
por Kelvin Brayan » Dom Mai 01, 2011 21:10
- 2 Respostas
- 3565 Exibições
- Última mensagem por Kelvin Brayan

Dom Mai 01, 2011 21:37
Álgebra Elementar
-
- Volume do cilindro e da esfera
por Pri Ferreira » Sex Mai 18, 2012 23:24
- 0 Respostas
- 2305 Exibições
- Última mensagem por Pri Ferreira

Sex Mai 18, 2012 23:24
Geometria Espacial
-
- [Cálculo do volume da esfera (coordenadas esféricas)]
por Horus123 » Qua Out 19, 2016 14:56
- 0 Respostas
- 4948 Exibições
- Última mensagem por Horus123

Qua Out 19, 2016 14:56
Cálculo: Limites, Derivadas e Integrais
-
- Por que a derivada do volume de uma esfera é igual a área?
por Therodrigou » Ter Abr 09, 2019 05:30
- 3 Respostas
- 14194 Exibições
- Última mensagem por Therodrigou

Ter Mai 05, 2020 04:25
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
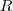 é dado por
é dado por 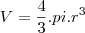 .
. .
. 

 .
. 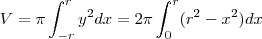

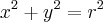
![y = \sqrt[]{r^{2} - x^{2}} y = \sqrt[]{r^{2} - x^{2}}](/latexrender/pictures/cd2d925abd7384eeabb03523959926e1.png) e x =[0, r]
e x =[0, r]![V = 2\pi\int_{0}^{r} \left[\sqrt[]{r^{2} - x^{2}} \right]^{2} dx = 2\pi\int_{0}^{r} r^{2} - x^{2} dx = V = 2\pi\int_{0}^{r} \left[\sqrt[]{r^{2} - x^{2}} \right]^{2} dx = 2\pi\int_{0}^{r} r^{2} - x^{2} dx =](/latexrender/pictures/c0a479dc9f74960a3d32e3005ceb5b24.png)