 por fabriel » Dom Mar 17, 2013 01:11
por fabriel » Dom Mar 17, 2013 01:11
Boa Noite pessoal.
Então acabei de ver um exercício aqui, mas estou em duvida quanto a resolução. É o seguinte:
O exercicio é Calcular a derivada dy/dx dessa função implícita aqui:
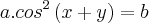
Meu inicio de resolução é da seguinte maneira:
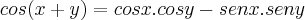
Então:
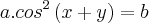

Derivando ambos os menbros temos:
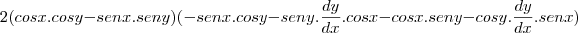
= 0
Mas isso resultara em um calculo muito extenso.. Existe outro caminho mais facilll??
Obrigado!!
Matemática, de modo algum, são fórmulas, assim como a música não são notas. (Y Jurquim)
-

fabriel
- Usuário Parceiro

-
- Mensagens: 88
- Registrado em: Ter Mai 22, 2012 16:04
- Localização: Chapadão do Sul-MS
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por e8group » Dom Mar 17, 2013 12:57
por e8group » Dom Mar 17, 2013 12:57
Vamos associar
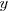
a

.
Então ,
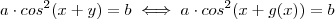
.
A igualdade acima só faz sentido
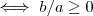
.Neste contexto, podemos dizer que ,
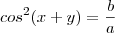
. E ainda ,considerando
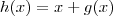
,temos
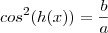
. Derivando implicitamente com respeito a

,
![[cos^2(h(x))]' = [\frac{b}{a}]' = 0 [cos^2(h(x))]' = [\frac{b}{a}]' = 0](/latexrender/pictures/2ac979eff30ef0ced92676dd8496f332.png)
.
De
![[cos^2(h(x))]' = 2 \cdot cos(h(x)) \cdot (-sin(h(x))\cdot h'(x) = - sin(2h(x)) \cdot h'(x) [cos^2(h(x))]' = 2 \cdot cos(h(x)) \cdot (-sin(h(x))\cdot h'(x) = - sin(2h(x)) \cdot h'(x)](/latexrender/pictures/2b3ddb6e4f05436aeb88f34d4faa8282.png)
e
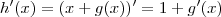
,segue que
![[cos^2(h(x))]' = - sin(2[x+g(x)]) \cdot (1 +g'(x)) [cos^2(h(x))]' = - sin(2[x+g(x)]) \cdot (1 +g'(x))](/latexrender/pictures/1fa610f673d33177e790458222077986.png)
.
Logo ,
![[cos^2(h(x))]' = 0 \iff g'(x) = - 1 [cos^2(h(x))]' = 0 \iff g'(x) = - 1](/latexrender/pictures/a3a6954dc371b8ac6ef365f1808bb8a1.png)
ou
![- sin(2[x+g(x)]) = 0 - sin(2[x+g(x)]) = 0](/latexrender/pictures/acb8f0ceaf364f48d74ea32e92454087.png)
.
Ou seja ,
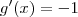
e
![2[x+g(x)] = k \cdot \pi , \forall k\in \mathbb{Z} \implies g(x) = - x + \frac{ k \cdot \pi }{2} , \forall k\in \mathbb{Z} 2[x+g(x)] = k \cdot \pi , \forall k\in \mathbb{Z} \implies g(x) = - x + \frac{ k \cdot \pi }{2} , \forall k\in \mathbb{Z}](/latexrender/pictures/9b8a4ac89e799665cefddc6c15c2c5c0.png)
, e de fato
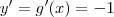
.
Tem gabarito ?
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por fabriel » Dom Mar 17, 2013 14:31
por fabriel » Dom Mar 17, 2013 14:31
Interessante!
Não tenho o gabarito, mas eu tinha feito daquele meu jeito, e tinha dado -1 também. Deve ser isso mesmo, pois de dois jeitos diferentes chegamos a um mesmo caso..
Obrigado!!
Matemática, de modo algum, são fórmulas, assim como a música não são notas. (Y Jurquim)
-

fabriel
- Usuário Parceiro

-
- Mensagens: 88
- Registrado em: Ter Mai 22, 2012 16:04
- Localização: Chapadão do Sul-MS
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por e8group » Dom Mar 17, 2013 14:39
por e8group » Dom Mar 17, 2013 14:39
OK . Acredito que está correto também .Utilizei o wolfram alpha para conferir a resolução ,mas ele reconheceu
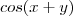
como uma função da forma
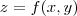
.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada] Ajuda com calculo de derivada de função quociente
por alienpuke » Dom Out 25, 2015 15:31
- 1 Respostas
- 12552 Exibições
- Última mensagem por Cleyson007

Dom Out 25, 2015 16:47
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada]derivada de função de raiz cúbica
por armando » Sáb Jul 20, 2013 15:22
- 4 Respostas
- 14792 Exibições
- Última mensagem por armando

Dom Jul 21, 2013 22:17
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Achar a derivada de uma função
por caiofisico » Seg Set 05, 2011 20:18
- 4 Respostas
- 3839 Exibições
- Última mensagem por caiofisico

Ter Set 06, 2011 19:44
Cálculo: Limites, Derivadas e Integrais
-
- ]Derivada de uma função] derivada com raiz
por Leandro_Araujo » Ter Mar 06, 2012 01:11
- 5 Respostas
- 8551 Exibições
- Última mensagem por LuizAquino

Ter Mar 06, 2012 13:40
Cálculo: Limites, Derivadas e Integrais
-
- derivada de uma função
por jmario » Sex Mai 07, 2010 13:51
- 4 Respostas
- 3795 Exibições
- Última mensagem por Elcioschin

Sex Mai 07, 2010 23:15
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
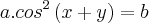
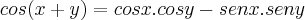
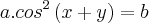

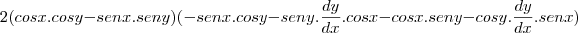 = 0
= 0

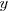 a
a  .
. 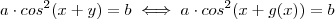 .
.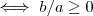 .Neste contexto, podemos dizer que ,
.Neste contexto, podemos dizer que , 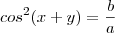 . E ainda ,considerando
. E ainda ,considerando 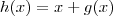 ,temos
,temos 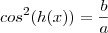 . Derivando implicitamente com respeito a
. Derivando implicitamente com respeito a  ,
, ![[cos^2(h(x))]' = [\frac{b}{a}]' = 0 [cos^2(h(x))]' = [\frac{b}{a}]' = 0](/latexrender/pictures/2ac979eff30ef0ced92676dd8496f332.png) .
. ![[cos^2(h(x))]' = 2 \cdot cos(h(x)) \cdot (-sin(h(x))\cdot h'(x) = - sin(2h(x)) \cdot h'(x) [cos^2(h(x))]' = 2 \cdot cos(h(x)) \cdot (-sin(h(x))\cdot h'(x) = - sin(2h(x)) \cdot h'(x)](/latexrender/pictures/2b3ddb6e4f05436aeb88f34d4faa8282.png) e
e 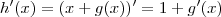 ,segue que
,segue que ![[cos^2(h(x))]' = - sin(2[x+g(x)]) \cdot (1 +g'(x)) [cos^2(h(x))]' = - sin(2[x+g(x)]) \cdot (1 +g'(x))](/latexrender/pictures/1fa610f673d33177e790458222077986.png) .
. ![[cos^2(h(x))]' = 0 \iff g'(x) = - 1 [cos^2(h(x))]' = 0 \iff g'(x) = - 1](/latexrender/pictures/a3a6954dc371b8ac6ef365f1808bb8a1.png) ou
ou ![- sin(2[x+g(x)]) = 0 - sin(2[x+g(x)]) = 0](/latexrender/pictures/acb8f0ceaf364f48d74ea32e92454087.png) .
. 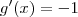 e
e ![2[x+g(x)] = k \cdot \pi , \forall k\in \mathbb{Z} \implies g(x) = - x + \frac{ k \cdot \pi }{2} , \forall k\in \mathbb{Z} 2[x+g(x)] = k \cdot \pi , \forall k\in \mathbb{Z} \implies g(x) = - x + \frac{ k \cdot \pi }{2} , \forall k\in \mathbb{Z}](/latexrender/pictures/9b8a4ac89e799665cefddc6c15c2c5c0.png) , e de fato
, e de fato 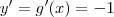 .
.
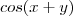 como uma função da forma
como uma função da forma 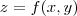 .
.
 .
.



