 por fabriel » Sex Mar 15, 2013 13:27
por fabriel » Sex Mar 15, 2013 13:27
Oi Pessoal estou com uma pequena duvida nesse exercicio:
Quero calcula a seguinte derivada da função implicita
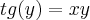
ai cheguei no seguinte:
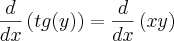
Ai cheguei nessa expressão:
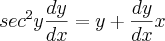
ou
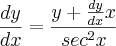
mas ai não consigo sair dessa expressão, eu errei em algum calculo??
Obrigado!!
Matemática, de modo algum, são fórmulas, assim como a música não são notas. (Y Jurquim)
-

fabriel
- Usuário Parceiro

-
- Mensagens: 88
- Registrado em: Ter Mai 22, 2012 16:04
- Localização: Chapadão do Sul-MS
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por e8group » Sex Mar 15, 2013 21:50
por e8group » Sex Mar 15, 2013 21:50
Usarei a seguinte notação

para derivada de primeira ordem com respeito a

. Somando-se
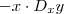
em ambos membros ,obtemos

,deixando em evidência
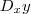
, segue
![[sec^2(y) - x] D_x y = y [sec^2(y) - x] D_x y = y](/latexrender/pictures/a46fd8085510cf44fce9876794bf6b5f.png)
; logo ,
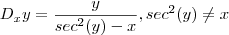
.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada] Função Implicita-duvidas na resoluão.
por fabriel » Dom Mar 17, 2013 01:11
- 3 Respostas
- 2080 Exibições
- Última mensagem por e8group

Dom Mar 17, 2013 14:39
Cálculo: Limites, Derivadas e Integrais
-
- Derivada Implícita
por ariclenesmelo » Ter Out 23, 2012 14:32
- 3 Respostas
- 2785 Exibições
- Última mensagem por young_jedi

Qui Out 25, 2012 22:33
Cálculo: Limites, Derivadas e Integrais
-
- Derivada Implicita
por Janoca » Dom Jun 22, 2014 02:40
- 3 Respostas
- 6913 Exibições
- Última mensagem por jugrigori

Dom Jun 03, 2018 16:05
Cálculo: Limites, Derivadas e Integrais
-
- [derivada implícita]exercício
por luiz_henriquear » Seg Out 24, 2011 20:48
- 5 Respostas
- 4111 Exibições
- Última mensagem por LuizAquino

Ter Nov 01, 2011 23:04
Cálculo: Limites, Derivadas e Integrais
-
- Dúvida - derivada implícita
por Danilo » Dom Out 13, 2013 22:31
- 2 Respostas
- 1922 Exibições
- Última mensagem por Danilo

Seg Out 14, 2013 01:32
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
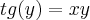
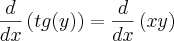
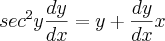
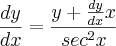

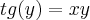
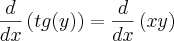
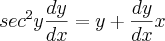
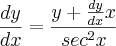

 para derivada de primeira ordem com respeito a
para derivada de primeira ordem com respeito a  . Somando-se
. Somando-se 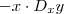 em ambos membros ,obtemos
em ambos membros ,obtemos  ,deixando em evidência
,deixando em evidência 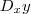 , segue
, segue ![[sec^2(y) - x] D_x y = y [sec^2(y) - x] D_x y = y](/latexrender/pictures/a46fd8085510cf44fce9876794bf6b5f.png) ; logo ,
; logo ,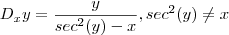 .
.
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.