O circuito é de 2 malhas e têm duas pilhas. Os valores são:
E a fonte 2 tem a resistência interna dezprezível e podemos considerá-la como fonte ideal.
1. Encontre as correntes elétricas do circuito. Os sentidos colocados na figura estão corretos? Corrija na figura.
2.Calcule a d.d.p entre os pontos Va-Vc e Vc-Vd.
3.Qual a quantidade de energia química da fonte é transformada em energia elétrica em três horas?
4. Qual energia útil fornecida pela fonte em três horas?
Ah! Num item eu disse que a pilha que funciona como fonte é a
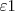e a que funciona como acumulador é a 
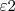, porque a voltagem é maior e menor, respectivamente. É isso?Obrigada!
, avisa que eu resolvo.
