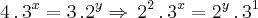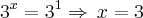por JKS » Qua Mar 06, 2013 18:12
por JKS » Qua Mar 06, 2013 18:12
não consigo fazer, já tentei substituir não chego a nenhuma resposta.. desde já agradeço..
(mackenzie-sp)Se os inteiros x e y satisfazem a equação

, então o valor de

é :
-
JKS
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Qua Ago 01, 2012 13:13
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por marinalcd » Qua Mar 06, 2013 18:22
por marinalcd » Qua Mar 06, 2013 18:22
JKS escreveu:não consigo fazer, já tentei substituir não chego a nenhuma resposta.. desde já agradeço..
(mackenzie-sp)Se os inteiros x e y satisfazem a equação

, então o valor de

é :
Primeiro vamos abrir o 3 e o 2:

Arrumando tudo, temos:

Por fim:

que é igual a
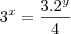
Espero ter ajudado!!
Poste o gabarito, para que eu possa confirmar o resultado!
E, repasse passo-a-passo!
-
marinalcd
- Colaborador Voluntário

-
- Mensagens: 143
- Registrado em: Sex Abr 27, 2012 21:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
 por JKS » Qui Mar 14, 2013 17:03
por JKS » Qui Mar 14, 2013 17:03
Me ajudou muito, mas ainda não consigo entender como o resultado no livro está dando
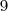
.. como ele descobriu que o x vale 2 ? . por favor se puder me ajudar de novo, ou descobrir o porque deu 9 eu agradeço ..
-
JKS
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Qua Ago 01, 2012 13:13
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por JKS » Dom Mar 17, 2013 13:04
por JKS » Dom Mar 17, 2013 13:04
Obrigadaa

-
JKS
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Qua Ago 01, 2012 13:13
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [potenciação] raiz cúbica com potenciação
por JKS » Qua Mar 06, 2013 17:41
- 2 Respostas
- 2287 Exibições
- Última mensagem por JKS

Qui Mar 14, 2013 16:43
Álgebra Linear
-
- (Mackenzie)
por my2009 » Sex Jan 28, 2011 21:28
- 1 Respostas
- 2689 Exibições
- Última mensagem por 0 kelvin

Sáb Jan 29, 2011 18:57
Logaritmos
-
- (Mackenzie) P.A. com P.G.
por Rafael16 » Sáb Ago 04, 2012 14:19
- 3 Respostas
- 10072 Exibições
- Última mensagem por MarceloFantini

Qui Set 13, 2012 10:20
Progressões
-
- Mackenzie
por Maria Livia » Qua Fev 27, 2013 22:29
- 1 Respostas
- 33667 Exibições
- Última mensagem por Cleyson007

Qua Fev 27, 2013 22:41
Geometria Espacial
-
- (MACKENZIE-SP)
por Thiago 86 » Qua Mar 27, 2013 23:23
- 4 Respostas
- 3209 Exibições
- Última mensagem por DanielFerreira

Sáb Abr 06, 2013 21:03
Inequações
Usuários navegando neste fórum: Nenhum usuário registrado e 11 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 , então o valor de
, então o valor de  é :
é :
 , então o valor de
, então o valor de  é :
é :
, então o valor de
é :



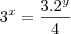

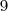 .. como ele descobriu que o x vale 2 ? . por favor se puder me ajudar de novo, ou descobrir o porque deu 9 eu agradeço ..
.. como ele descobriu que o x vale 2 ? . por favor se puder me ajudar de novo, ou descobrir o porque deu 9 eu agradeço ..