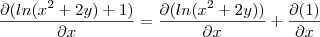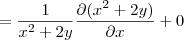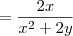por Sobreira » Qua Mar 13, 2013 00:59
por Sobreira » Qua Mar 13, 2013 00:59
Prezados,
Resolvi a derivada parcial, em relação a x, abaixo e o meu valor não bate com o do livro.
Segue a resolução e a resposta do livro.
![f(x,y)=\sqrt[]{Ln\left({x}^{2}+2y \right)+1} f(x,y)=\sqrt[]{Ln\left({x}^{2}+2y \right)+1}](/latexrender/pictures/f2cd273ffe59f3ef6a7b79b90f675b4e.png)
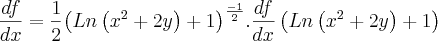
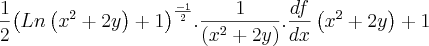
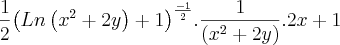

![\frac{x+1}{\sqrt[]{Ln\left({x}^{2}+2y \right)+1}.\left({x}^{2}+2y \right)} \frac{x+1}{\sqrt[]{Ln\left({x}^{2}+2y \right)+1}.\left({x}^{2}+2y \right)}](/latexrender/pictures/9bb2999f479756596b425b34a1b91fcd.png)
O livro apresenta como resposta:
![\frac{x}{\sqrt[]{Ln\left({x}^{2}+2y \right)+1}.\left({x}^{2}+2y \right)} \frac{x}{\sqrt[]{Ln\left({x}^{2}+2y \right)+1}.\left({x}^{2}+2y \right)}](/latexrender/pictures/36662203596d5bccdfec5e70cc864d1b.png)
O que eu reparei foi que o livro derivou este "+1", mas eu não entendo o seguinte, se este termo não está dentro dos parenteses porque devo deriva-lo também?
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por young_jedi » Qui Mar 14, 2013 11:15
por young_jedi » Qui Mar 14, 2013 11:15
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada] Regra da cadeia
por gabriel feron » Seg Out 01, 2012 23:08
- 1 Respostas
- 1588 Exibições
- Última mensagem por young_jedi

Seg Out 01, 2012 23:16
Cálculo: Limites, Derivadas e Integrais
-
- [DERIVADA] regra da cadeia
por tatianaCAL » Sáb Jun 22, 2013 09:47
- 1 Respostas
- 1494 Exibições
- Última mensagem por young_jedi

Sáb Jun 22, 2013 11:33
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada - Regra de Cadeia]
por anner » Sex Jul 04, 2014 00:14
- 2 Respostas
- 3091 Exibições
- Última mensagem por Daniela[

Sáb Jul 05, 2014 14:40
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada]regra da cadeia
por principiante » Dom Fev 04, 2018 10:28
- 1 Respostas
- 5040 Exibições
- Última mensagem por Baltuilhe

Dom Fev 04, 2018 21:02
Cálculo: Limites, Derivadas e Integrais
-
- Derivada pela regra da cadeia
por Priscila_moraes » Ter Dez 06, 2011 12:48
- 3 Respostas
- 2985 Exibições
- Última mensagem por MarceloFantini

Ter Dez 06, 2011 15:38
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 16 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![f(x,y)=\sqrt[]{Ln\left({x}^{2}+2y \right)+1} f(x,y)=\sqrt[]{Ln\left({x}^{2}+2y \right)+1}](/latexrender/pictures/f2cd273ffe59f3ef6a7b79b90f675b4e.png)
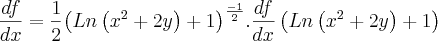
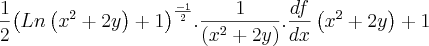
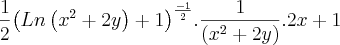

![\frac{x+1}{\sqrt[]{Ln\left({x}^{2}+2y \right)+1}.\left({x}^{2}+2y \right)} \frac{x+1}{\sqrt[]{Ln\left({x}^{2}+2y \right)+1}.\left({x}^{2}+2y \right)}](/latexrender/pictures/9bb2999f479756596b425b34a1b91fcd.png)
![\frac{x}{\sqrt[]{Ln\left({x}^{2}+2y \right)+1}.\left({x}^{2}+2y \right)} \frac{x}{\sqrt[]{Ln\left({x}^{2}+2y \right)+1}.\left({x}^{2}+2y \right)}](/latexrender/pictures/36662203596d5bccdfec5e70cc864d1b.png)