 por Thiago 86 » Ter Mar 12, 2013 15:00
por Thiago 86 » Ter Mar 12, 2013 15:00
Saldações

, estou respondendo uma questão e infelismente não consigo descobrí onde estou errando.
Para que valores de "m" a equação

, admite raizes reais simétricas.
1° dúvida. O termo simetria usado, significa igualdade?
Como eu tentei:
![{x}^{2} - (m-2)x-9=0
\Delta=0
{[-(m-2)]}^{2} - 4.1.(-9)=0
{m}^{2} -4m+4+36=0
{m}^{2} -4m+40=0
\Delta={-4}^{2} -4.1.40
\Delta=16-160
\Delta=-144??? {x}^{2} - (m-2)x-9=0
\Delta=0
{[-(m-2)]}^{2} - 4.1.(-9)=0
{m}^{2} -4m+4+36=0
{m}^{2} -4m+40=0
\Delta={-4}^{2} -4.1.40
\Delta=16-160
\Delta=-144???](/latexrender/pictures/73ebd5180ac87d0a253a44a107e4465c.png)
-
Thiago 86
- Usuário Dedicado

-
- Mensagens: 40
- Registrado em: Seg Fev 11, 2013 18:55
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Curso técnico em enfermagem
- Andamento: cursando
 por Russman » Ter Mar 12, 2013 16:49
por Russman » Ter Mar 12, 2013 16:49
Não! Números simétricos tem o mesmo módulo, mas sinais opostos. O simétrico de

é

.
Assim, as raízes da equação tem de ser

e
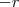
. Há diversas formas de resolver essa questão. Optei por esta:
A equação tem raízes

e
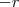
. Assim, podemos escreve-la como

de forma que
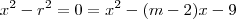
.
Por igualdade de polinômios, temos, então
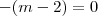
, de onde
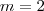
, e

.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Thiago 86 » Qua Mar 13, 2013 09:39
por Thiago 86 » Qua Mar 13, 2013 09:39
Saudações

.
Descupe-me, mas eu não sei o que é números simétricose.
Eu estou estudando matemática sozinho, desde o início com uma apostila, e estou vendo que ela tem algumas falhas se você tivesse algum material falando sobrre simetria que pudece me enviar ficaria agradecido.
Voltando para a questão, é por isso que eu não consegui entender porque x=-x.
Desde já muito obrigado.
-
Thiago 86
- Usuário Dedicado

-
- Mensagens: 40
- Registrado em: Seg Fev 11, 2013 18:55
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Curso técnico em enfermagem
- Andamento: cursando
Voltar para Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 , estou respondendo uma questão e infelismente não consigo descobrí onde estou errando.
, estou respondendo uma questão e infelismente não consigo descobrí onde estou errando. , admite raizes reais simétricas.
, admite raizes reais simétricas.![{x}^{2} - (m-2)x-9=0
\Delta=0
{[-(m-2)]}^{2} - 4.1.(-9)=0
{m}^{2} -4m+4+36=0
{m}^{2} -4m+40=0
\Delta={-4}^{2} -4.1.40
\Delta=16-160
\Delta=-144??? {x}^{2} - (m-2)x-9=0
\Delta=0
{[-(m-2)]}^{2} - 4.1.(-9)=0
{m}^{2} -4m+4+36=0
{m}^{2} -4m+40=0
\Delta={-4}^{2} -4.1.40
\Delta=16-160
\Delta=-144???](/latexrender/pictures/73ebd5180ac87d0a253a44a107e4465c.png)

 , estou respondendo uma questão e infelismente não consigo descobrí onde estou errando.
, estou respondendo uma questão e infelismente não consigo descobrí onde estou errando. , admite raizes reais simétricas.
, admite raizes reais simétricas.![{x}^{2} - (m-2)x-9=0
\Delta=0
{[-(m-2)]}^{2} - 4.1.(-9)=0
{m}^{2} -4m+4+36=0
{m}^{2} -4m+40=0
\Delta={-4}^{2} -4.1.40
\Delta=16-160
\Delta=-144??? {x}^{2} - (m-2)x-9=0
\Delta=0
{[-(m-2)]}^{2} - 4.1.(-9)=0
{m}^{2} -4m+4+36=0
{m}^{2} -4m+40=0
\Delta={-4}^{2} -4.1.40
\Delta=16-160
\Delta=-144???](/latexrender/pictures/73ebd5180ac87d0a253a44a107e4465c.png)

 é
é  .
. e
e 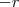 . Há diversas formas de resolver essa questão. Optei por esta:
. Há diversas formas de resolver essa questão. Optei por esta: e
e 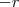 . Assim, podemos escreve-la como
. Assim, podemos escreve-la como
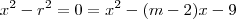 .
.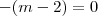 , de onde
, de onde 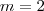 , e
, e  .
.
 .
.


 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.