 por laura_biscaro » Ter Mar 12, 2013 16:15
por laura_biscaro » Ter Mar 12, 2013 16:15
Simplifique a expressão:
A =

é uma questão meio ridícula, mas não consigo resolver :/
-
laura_biscaro
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Seg Fev 18, 2013 19:05
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Douglas16 » Ter Mar 12, 2013 16:29
por Douglas16 » Ter Mar 12, 2013 16:29
Tipo, é como esta igualdade diz:

E de forma análoga os outros termos, então encontre o termo comum que existe entre o numerador e denominador e elimine este termo, tipo:

Aqui o termo comum é o
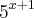
colocando-o em evidência, ou seja fatorando em termos de
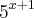
, fica:
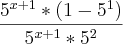
=
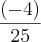
=

Veja que eu eliminei o termo
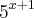
dividindo o
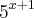
do numerador com o
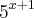
do denominador.
-
Douglas16
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Fev 11, 2013 19:15
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por laura_biscaro » Ter Mar 12, 2013 16:51
por laura_biscaro » Ter Mar 12, 2013 16:51
muito bem, então, seguindo seu raciocínio, a equação ficaria:
A =

o que resultaria em:
A =
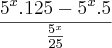
certo?
-
laura_biscaro
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Seg Fev 18, 2013 19:05
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Russman » Ter Mar 12, 2013 16:54
por Russman » Ter Mar 12, 2013 16:54
Certo!
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por laura_biscaro » Ter Mar 12, 2013 17:06
por laura_biscaro » Ter Mar 12, 2013 17:06
beleza. o resultado dá 3000.
muito obrigada, gente!
-
laura_biscaro
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Seg Fev 18, 2013 19:05
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Russman » Ter Mar 12, 2013 17:19
por Russman » Ter Mar 12, 2013 17:19
Isso mesmo. (:
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvida Potenciação
por sullivan » Sex Dez 23, 2011 10:21
- 4 Respostas
- 3012 Exibições
- Última mensagem por sullivan

Sex Dez 23, 2011 13:26
Álgebra Elementar
-
- Dúvida - potenciação
por Danilo » Qua Ago 29, 2012 10:27
- 6 Respostas
- 3518 Exibições
- Última mensagem por LuizAquino

Qua Ago 29, 2012 18:15
Números Complexos
-
- Dúvida em Potenciação Urgente
por Kelvin Brayan » Seg Mai 09, 2011 02:52
- 2 Respostas
- 2019 Exibições
- Última mensagem por Kelvin Brayan

Seg Mai 09, 2011 10:56
Álgebra Elementar
-
- [Duvida] Potenciação [Sinal]
por MiyaChan » Qua Jun 01, 2016 19:15
- 3 Respostas
- 4257 Exibições
- Última mensagem por Cleyson007

Dom Jun 05, 2016 11:02
Sequências
-
- Duvida em alguns exercícios de potenciação
por GiovaniF » Ter Mar 19, 2013 14:14
- 1 Respostas
- 1471 Exibições
- Última mensagem por timoteo

Ter Mar 19, 2013 21:51
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.






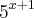
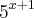 , fica:
, fica: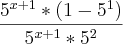 =
=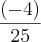 =
=
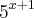 dividindo o
dividindo o 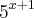 do numerador com o
do numerador com o 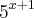 do denominador.
do denominador.

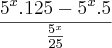




 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.