 por Douglas16 » Sex Mar 08, 2013 17:33
por Douglas16 » Sex Mar 08, 2013 17:33
![\lim_{x\rightarrow2} \frac{x*x-4}{x-[x]} \lim_{x\rightarrow2} \frac{x*x-4}{x-[x]}](/latexrender/pictures/d9741e463c448f35490c06dc13f403aa.png)
Onde [x] é maior número inteiro que é menor ou igual a x.
Minha resolução:
1º.
![\lim_{x\rightarrow{2}^{+}} \frac{x*x-4}{x-[x]}=\lim_{x\rightarrow{2}^{+}} \frac{x*x-4}{x-2}=\lim_{x\rightarrow{2}^{+}} \frac{(x+2)(x-2)}{(x-2)}=\lim_{x\rightarrow{2}^{+}} (x+2)=4 \lim_{x\rightarrow{2}^{+}} \frac{x*x-4}{x-[x]}=\lim_{x\rightarrow{2}^{+}} \frac{x*x-4}{x-2}=\lim_{x\rightarrow{2}^{+}} \frac{(x+2)(x-2)}{(x-2)}=\lim_{x\rightarrow{2}^{+}} (x+2)=4](/latexrender/pictures/23596568f1503a32058c810094e3339a.png)
2º.
![\lim_{x\rightarrow{2}^{-}} \frac{x*x-4}{x-[x]}=\lim_{x\rightarrow{2}^{-}} \frac{x*x-4}{x-1}=0 \lim_{x\rightarrow{2}^{-}} \frac{x*x-4}{x-[x]}=\lim_{x\rightarrow{2}^{-}} \frac{x*x-4}{x-1}=0](/latexrender/pictures/4181ca24a4cd06144a3424f3207f4b78.png)
Portanto o limite não existe.
Está correto?
-
Douglas16
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Fev 11, 2013 19:15
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por e8group » Dom Mar 10, 2013 10:57
por e8group » Dom Mar 10, 2013 10:57
Bom dia ,temos uma função da forma
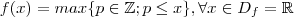
,para todo

em
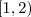
e

,respectivamente ,

e

.
Considerando
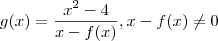
.
Quando

e
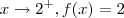
.
Conclusão : você está correto , realmente os limites laterais diferem (sendo um deles

e

) e portanto o limite de

,

, não existe .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Será que está correta a resolução e o resultado
por Douglas16 » Dom Mar 10, 2013 16:55
- 3 Respostas
- 4714 Exibições
- Última mensagem por Douglas16

Dom Mar 10, 2013 23:37
Cálculo: Limites, Derivadas e Integrais
-
- [Álgebra I, exercicios] Exercicios que estão sem resolução.
por vitorullmann » Ter Mar 05, 2013 21:26
- 0 Respostas
- 3293 Exibições
- Última mensagem por vitorullmann

Ter Mar 05, 2013 21:26
Álgebra Elementar
-
- [Razões e Proporções] Dúvida na resolução e resultado
por chenz » Sex Set 04, 2015 17:54
- 1 Respostas
- 4273 Exibições
- Última mensagem por nakagumahissao

Qua Out 07, 2015 13:01
Teoria dos Números
-
- Ajuda para provar que 3 pontos estão alinhados.
por Danilo » Qua Mai 02, 2012 02:08
- 1 Respostas
- 2378 Exibições
- Última mensagem por Russman

Qua Mai 02, 2012 06:19
Geometria Analítica
-
- [Equação} meus resultados ñ estão certos me ajudem
por teilom » Dom Jul 07, 2013 13:20
- 1 Respostas
- 950 Exibições
- Última mensagem por Leticia_alves

Dom Jul 07, 2013 18:04
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x\rightarrow2} \frac{x*x-4}{x-[x]} \lim_{x\rightarrow2} \frac{x*x-4}{x-[x]}](/latexrender/pictures/d9741e463c448f35490c06dc13f403aa.png)
![\lim_{x\rightarrow{2}^{+}} \frac{x*x-4}{x-[x]}=\lim_{x\rightarrow{2}^{+}} \frac{x*x-4}{x-2}=\lim_{x\rightarrow{2}^{+}} \frac{(x+2)(x-2)}{(x-2)}=\lim_{x\rightarrow{2}^{+}} (x+2)=4 \lim_{x\rightarrow{2}^{+}} \frac{x*x-4}{x-[x]}=\lim_{x\rightarrow{2}^{+}} \frac{x*x-4}{x-2}=\lim_{x\rightarrow{2}^{+}} \frac{(x+2)(x-2)}{(x-2)}=\lim_{x\rightarrow{2}^{+}} (x+2)=4](/latexrender/pictures/23596568f1503a32058c810094e3339a.png)
![\lim_{x\rightarrow{2}^{-}} \frac{x*x-4}{x-[x]}=\lim_{x\rightarrow{2}^{-}} \frac{x*x-4}{x-1}=0 \lim_{x\rightarrow{2}^{-}} \frac{x*x-4}{x-[x]}=\lim_{x\rightarrow{2}^{-}} \frac{x*x-4}{x-1}=0](/latexrender/pictures/4181ca24a4cd06144a3424f3207f4b78.png)

![\lim_{x\rightarrow2} \frac{x*x-4}{x-[x]} \lim_{x\rightarrow2} \frac{x*x-4}{x-[x]}](/latexrender/pictures/d9741e463c448f35490c06dc13f403aa.png)
![\lim_{x\rightarrow{2}^{+}} \frac{x*x-4}{x-[x]}=\lim_{x\rightarrow{2}^{+}} \frac{x*x-4}{x-2}=\lim_{x\rightarrow{2}^{+}} \frac{(x+2)(x-2)}{(x-2)}=\lim_{x\rightarrow{2}^{+}} (x+2)=4 \lim_{x\rightarrow{2}^{+}} \frac{x*x-4}{x-[x]}=\lim_{x\rightarrow{2}^{+}} \frac{x*x-4}{x-2}=\lim_{x\rightarrow{2}^{+}} \frac{(x+2)(x-2)}{(x-2)}=\lim_{x\rightarrow{2}^{+}} (x+2)=4](/latexrender/pictures/23596568f1503a32058c810094e3339a.png)
![\lim_{x\rightarrow{2}^{-}} \frac{x*x-4}{x-[x]}=\lim_{x\rightarrow{2}^{-}} \frac{x*x-4}{x-1}=0 \lim_{x\rightarrow{2}^{-}} \frac{x*x-4}{x-[x]}=\lim_{x\rightarrow{2}^{-}} \frac{x*x-4}{x-1}=0](/latexrender/pictures/4181ca24a4cd06144a3424f3207f4b78.png)

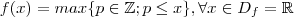 ,para todo
,para todo  em
em 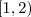 e
e  ,respectivamente ,
,respectivamente , e
e  .
. 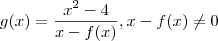 .
.  e
e 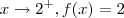 .
.  e
e  ) e portanto o limite de
) e portanto o limite de  ,
,  , não existe .
, não existe .