 por shirata » Seg Out 05, 2009 12:26
por shirata » Seg Out 05, 2009 12:26
(ITA -SP) O valor de "n" que torna a sequencia (2 + 3n, -5n, 1- 4n) uma progressão aritmetica pertence ao intervalo:
a) [-2, -1]
b) [-1, 0]
c) [0,1]
d) [1,2]
e) [2,3]
tentei dividir os termos cada um pelo seu anterior dessa forma: 1 - 4n/-5n = -5n/2 + 3n, já que a razão deve ser igual.
cheguei na equação
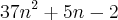
-
shirata
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Seg Out 05, 2009 11:25
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Seg Out 05, 2009 15:16
por Molina » Seg Out 05, 2009 15:16
Boa tarde.
Primeiramente vou dar uma dica, vamos ver se você consegue a partir daí:
Note que:



e


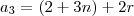
Só que temos o valor de

e
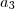
, então vamos substituir...
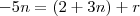

Agora deixe n de um lado e o número e o r de outro lado da igualdade.
Assim você terá 2 equações com duas variáveis.
Monte um sistema e encontre n.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Cleyson007 » Seg Out 05, 2009 18:41
por Cleyson007 » Seg Out 05, 2009 18:41
Boa tarde Shirata!
Seja bem vindo (a) ao Ajuda Matemática!
Quanto à resolução do problema proposto:


Resolvendo:
 Logo, n pertence ao intervalo [-1,0]. (Alternativa b)
Logo, n pertence ao intervalo [-1,0]. (Alternativa b)Comente qualquer dúvida

Até mais.
Um abraço.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Exercício sobre triângulos
 por LuizCarlos » Sáb Mar 31, 2012 17:12
por LuizCarlos » Sáb Mar 31, 2012 17:12
- 7 Respostas
- 7484 Exibições
- Última mensagem por LuizCarlos

Sáb Mar 31, 2012 18:53
Trigonometria
-
- Exercício sobre cone
por Calulodu » Dom Jun 02, 2013 23:12
- 1 Respostas
- 1886 Exibições
- Última mensagem por Calulodu

Seg Jun 03, 2013 20:01
Geometria Espacial
-
- Exercício sobre Limites !
por matheusfroes » Seg Abr 07, 2014 15:49
- 1 Respostas
- 2467 Exibições
- Última mensagem por Russman

Seg Abr 07, 2014 19:00
Cálculo: Limites, Derivadas e Integrais
-
- Dúvida sobre Exercício Conjunto
por Jhosmy » Qua Jun 01, 2011 15:14
- 6 Respostas
- 3788 Exibições
- Última mensagem por Jhosmy

Sáb Jun 04, 2011 00:42
Conjuntos
-
- Dúvida sobre a resolução de um exercício
por Danilo » Qua Jul 25, 2012 12:15
- 1 Respostas
- 1396 Exibições
- Última mensagem por Danilo

Qua Jul 25, 2012 12:35
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
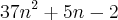

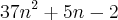






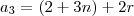
 e
e 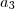 , então vamos substituir...
, então vamos substituir...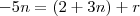








 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.