 por samysoares » Qua Mar 06, 2013 12:55
por samysoares » Qua Mar 06, 2013 12:55
Seja f uma função diferenciável e g uma função definida por
![g\left(x \right)=xf\left(\sqrt[]{x} \right) g\left(x \right)=xf\left(\sqrt[]{x} \right)](/latexrender/pictures/1c28716795eda1ca2d8e5abcc79de12a.png)
. Sabe-se que a reta tangente ao gráfico de g no ponto de abcissa 4 é perpendicular à reta y= -1/2x+5 e que f(2)=1. Calcule f'(2)
Por favor, quero dicas de como resolver.
-
samysoares
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Ter Jan 08, 2013 12:42
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Russman » Qua Mar 06, 2013 15:06
por Russman » Qua Mar 06, 2013 15:06
samysoares escreveu:Sabe-se que a reta tangente ao gráfico de g no ponto de abcissa 4 é perpendicular à reta y= -1/2x+5
Deste trecho você pode calcular o valor de
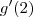
.
Sabendo o valor de
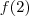
, que é dado, é muito simples isolar o valor pedido.
Veja que, se
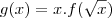
então
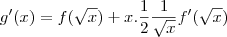
e fazendo

, tomando

, você resolve o problema.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- probleminha
por leandro moraes » Seg Mai 30, 2011 08:06
- 1 Respostas
- 1794 Exibições
- Última mensagem por carlosalesouza

Seg Mai 30, 2011 09:34
Cálculo: Limites, Derivadas e Integrais
-
- probleminha 2
por leandro moraes » Ter Mai 31, 2011 14:41
- 1 Respostas
- 2775 Exibições
- Última mensagem por carlosalesouza

Ter Mai 31, 2011 17:42
Cálculo: Limites, Derivadas e Integrais
-
- Probleminha
por Pjrleal » Qua Mar 14, 2012 10:11
- 1 Respostas
- 2890 Exibições
- Última mensagem por LuizAquino

Qua Mar 14, 2012 15:42
Álgebra Elementar
-
- Probleminha
por karen » Ter Nov 27, 2012 15:55
- 2 Respostas
- 2166 Exibições
- Última mensagem por karen

Ter Nov 27, 2012 16:22
Álgebra Elementar
-
- Probleminha de datas
por ginrj » Seg Jun 22, 2009 17:45
- 2 Respostas
- 2024 Exibições
- Última mensagem por ginrj

Seg Jun 22, 2009 18:11
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![g\left(x \right)=xf\left(\sqrt[]{x} \right) g\left(x \right)=xf\left(\sqrt[]{x} \right)](/latexrender/pictures/1c28716795eda1ca2d8e5abcc79de12a.png) . Sabe-se que a reta tangente ao gráfico de g no ponto de abcissa 4 é perpendicular à reta y= -1/2x+5 e que f(2)=1. Calcule f'(2)
. Sabe-se que a reta tangente ao gráfico de g no ponto de abcissa 4 é perpendicular à reta y= -1/2x+5 e que f(2)=1. Calcule f'(2)
![g\left(x \right)=xf\left(\sqrt[]{x} \right) g\left(x \right)=xf\left(\sqrt[]{x} \right)](/latexrender/pictures/1c28716795eda1ca2d8e5abcc79de12a.png) . Sabe-se que a reta tangente ao gráfico de g no ponto de abcissa 4 é perpendicular à reta y= -1/2x+5 e que f(2)=1. Calcule f'(2)
. Sabe-se que a reta tangente ao gráfico de g no ponto de abcissa 4 é perpendicular à reta y= -1/2x+5 e que f(2)=1. Calcule f'(2)
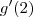 .
.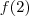 , que é dado, é muito simples isolar o valor pedido.
, que é dado, é muito simples isolar o valor pedido.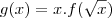
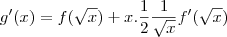
 , tomando
, tomando  , você resolve o problema.
, você resolve o problema.
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.