 por ruisu » Seg Mar 04, 2013 15:19
por ruisu » Seg Mar 04, 2013 15:19
Eu achei uma questão na internet, e só dizia isso:

? M(b-a)
M = máx |f(x)| x E [a,b]
-
ruisu
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sáb Mar 02, 2013 20:13
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Computação
- Andamento: cursando
 por young_jedi » Seg Mar 04, 2013 23:14
por young_jedi » Seg Mar 04, 2013 23:14
se M é o valor maximo de f(x) para qualquer valor de x entre (a,b) então
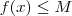
portanto
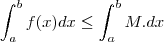
como M é um valor constante


com isso voce demonstra oque se queria
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Ponto Máximo e Mínimo de uma função.
por lucasowner » Qui Ago 13, 2015 03:05
- 1 Respostas
- 2007 Exibições
- Última mensagem por nakagumahissao

Qui Ago 13, 2015 15:29
Cálculo: Limites, Derivadas e Integrais
-
- [Ponto máximo de uma função]- Pressão sanguínea.
por alicemneves » Seg Mai 28, 2012 00:20
- 7 Respostas
- 5362 Exibições
- Última mensagem por Russman

Qui Mai 31, 2012 22:58
Cálculo: Limites, Derivadas e Integrais
-
- Pontos maximo e minimos de uma funçao e ponto de sela
por b11adriano » Sáb Out 04, 2014 14:56
- 2 Respostas
- 2823 Exibições
- Última mensagem por Marcos Ueder

Qui Set 17, 2015 18:09
Cálculo: Limites, Derivadas e Integrais
-
- Ponto Máximo
por Ana_Bela » Qui Nov 27, 2014 11:08
- 1 Respostas
- 1373 Exibições
- Última mensagem por adauto martins

Qui Nov 27, 2014 11:46
Funções
-
- Derivada através de Ponto Máximo - Otimização
por Suriano » Qua Mai 06, 2009 20:42
- 3 Respostas
- 6214 Exibições
- Última mensagem por Suriano

Qua Mai 13, 2009 21:39
Cálculo
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 ? M(b-a)
? M(b-a)
 ? M(b-a)
? M(b-a)
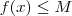
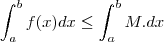




 .
.
 :
: