 por OoluanOo » Dom Mar 03, 2013 18:02
por OoluanOo » Dom Mar 03, 2013 18:02
PESSOAL TENHO DOIS EXERCICIOS DE TAXA DE VARIAÇÃO QUE NÃO CONSIGO FAZER, POR FAVOR ME AJUDEM COM ESSES EXERCICIOS POIS TEREI PROVA RELACIONADO A ESSE ASSUNTO E QUERIA VER A RESOLUÇÃO DESSAS 2 QUESTÕES! DESDE JÁ OBRIGADO.
1 - Um balão está a 60 m acima do solo e se eleva verticalmente à razão de 5 m/s. Um automóvel
passa por baixo do balão viajando à 12 m/s. Com que velocidade varia, um segundo depois, a
distância entre o balão e o automóvel?
2 - Despeja-se água num recipiente de forma cônica, à razão de 8 cm3/min. O cone tem 20 cm de
profundidade e 10 cm de diâmetro em sua parte superior. Se existe um furo na base, e o nível da
água está subindo à razão de 1 mm/min, com que velocidade a água estará escoando quando esta
estiver a 16 cm do fundo?
-
OoluanOo
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Mar 03, 2013 17:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Exatas/Ciencia da Computação
- Andamento: cursando
 por Russman » Dom Mar 03, 2013 19:58
por Russman » Dom Mar 03, 2013 19:58
Para resolver esse tipo de questão você precisa, primeiramente, identificar qual grandeza deve ser calculada sua taxa de variação. Feito isso, você deve estabelecer, ou identificar, uma relação matemática entre essa grandeza e as outras envolvidas no problema. Vou começar a 1°questão e você tente completar a solução.
Colocando o carro a mover-se sobre uma linha vertical, imaginando ser esta o solo, e o balão a mover-se em uma vertical temos em carro+balão+solo um triângulo retângulo. Assim, o quadrado da distância entre o balão o carro será a soma do quadrado da distância entre carro e a linha vertical do balão com o quadrado da altura do balão. Veja que identificamos primeiro a grandeza a ser derivada - a distância entre o balão e o carro - e depois estabelecemos uma relação matemática entre ela e as outras grandezas do problema - movimento vertical do balão e horizontal do carro.
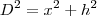

: distancia entre eles.

: distancia do carro a vertical do balão.

: altura do balão.
Agora tome a derivada em ambos os lado e prossiga.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada] Taxa de variação
por Aliocha Karamazov » Sáb Nov 26, 2011 18:40
- 3 Respostas
- 8063 Exibições
- Última mensagem por MarceloFantini

Dom Nov 27, 2011 01:57
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Taxa de Variação
por Vanny » Dom Set 30, 2012 20:58
- 0 Respostas
- 3113 Exibições
- Última mensagem por Vanny

Dom Set 30, 2012 20:58
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] - Taxa de Variação
por Jeks_Osodrac » Ter Jul 30, 2013 19:19
- 3 Respostas
- 3272 Exibições
- Última mensagem por Russman

Qua Jul 31, 2013 18:03
Cálculo: Limites, Derivadas e Integrais
-
- Derivada como Taxa de Variação
por Ronaldobb » Sex Set 21, 2012 20:29
- 3 Respostas
- 2265 Exibições
- Última mensagem por MarceloFantini

Sáb Set 22, 2012 00:05
Cálculo: Limites, Derivadas e Integrais
-
- Derivada - Taxa de variação - velocidade
por emanes » Qua Out 17, 2012 11:10
- 1 Respostas
- 3930 Exibições
- Última mensagem por young_jedi

Qua Out 17, 2012 11:50
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


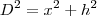
 : distancia entre eles.
: distancia entre eles. : distancia do carro a vertical do balão.
: distancia do carro a vertical do balão. : altura do balão.
: altura do balão. 
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  .
.
