 por Pento » Dom Mar 03, 2013 16:06
por Pento » Dom Mar 03, 2013 16:06
Gostaria de obter algum exemplo de exercício resolvido,uma explicação clara de como resolver,ex.um inteiro três quarto por cento de quatro mil e oitocentos,pagar ainda sobre dois inteiro e um meio por mil.
-
Pento
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Mar 03, 2013 13:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: ciencias contabeis
- Andamento: cursando
 por Douglas16 » Dom Mar 03, 2013 16:19
por Douglas16 » Dom Mar 03, 2013 16:19
Talvez se escrever com números e frações fique mais claro de entender o que você quiz dizer. Tipo você pode escrever "um por cento" deste modo:

.
Para isso clique no botão editor de fórmulas.
-
Douglas16
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Fev 11, 2013 19:15
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por Pento » Dom Mar 03, 2013 19:27
por Pento » Dom Mar 03, 2013 19:27
Não consigo digita de formA de fração
1 2/3%,2 1/2 por mil
-
Pento
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Mar 03, 2013 13:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: ciencias contabeis
- Andamento: cursando
 por Douglas16 » Seg Mar 04, 2013 13:19
por Douglas16 » Seg Mar 04, 2013 13:19
Se foi isso que quis dizer:
um inteiro três quarto por cento de quatro mil e oitocentos é:
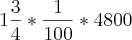

agora 'pagar' é que eu não sei o que tem haver com 'ainda sobre dois inteiro e um meio por mil que é:

'.
Se foi isso ou não, eu não sei, mas se você tiver dúvida de como fazer operações com frações, então avisa aqui no fórum ou tente encontrar algo já postado.
-
Douglas16
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Fev 11, 2013 19:15
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Matemática Financeira
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- expressão fracionária
por Andreza » Sex Jan 06, 2012 16:49
- 4 Respostas
- 2204 Exibições
- Última mensagem por DanielFerreira

Sáb Jan 07, 2012 21:17
Álgebra Elementar
-
- [Integral] Fracionária
por klueger » Ter Mar 05, 2013 12:22
- 2 Respostas
- 1856 Exibições
- Última mensagem por klueger

Ter Mar 05, 2013 13:19
Cálculo: Limites, Derivadas e Integrais
-
- Resolvendo Equação Fracionária com MMC
por rapharocket » Qui Mar 03, 2011 16:28
- 0 Respostas
- 2530 Exibições
- Última mensagem por rapharocket

Qui Mar 03, 2011 16:28
Sistemas de Equações
-
- Inequação logaritmica com base fracionária
por petras » Qua Out 26, 2016 13:38
- 0 Respostas
- 2444 Exibições
- Última mensagem por petras

Qua Out 26, 2016 13:38
Logaritmos
-
- Equação Fracionária do Segundo Grau Ajuda Urgente
 por karenblond » Ter Ago 18, 2015 11:17
por karenblond » Ter Ago 18, 2015 11:17
- 6 Respostas
- 8159 Exibições
- Última mensagem por nakagumahissao

Ter Ago 18, 2015 18:17
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 .
.

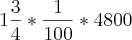

 '.
'.
