Dúvidas pendentes de estatística ou outras áreas (física, química etc), aguardando bacharéis dispostos e habilitados a ajudar.
Regras do fórum
- Não envie somente enunciados de problemas, informe suas tentativas e dificuldades!
Queremos que a "ajuda" represente um trabalho interativo, pois saber especificar a dúvida exige estudo.
Serão desconsiderados tópicos apenas com enunciados, sem interação. Nosso objetivo não é resolver listas de exercícios;
- Para não haver má interpretação em suas postagens, especialmente na precedência das operações, utilize LaTeX, podendo ser a partir do botão "editor de fórmulas".
Bons estudos!
 por tatimamedes » Sex Mar 01, 2013 00:57
por tatimamedes » Sex Mar 01, 2013 00:57
Estou com dúvida no seguinte exercício:
Uma caixa contém 20 canetas iguais, das quais 7 são defeituosas, e outra caixa contém 12, das quais 4 são defeituosas. Uma caneta é retirada aleatoriamente de cada caixa. As probabilidades de que ambas não sejam defeituosas e de que uma seja perfeita e a outra não são respectivamente de:
A. 88,33% e 45,00%
B. 43,33% e 45,00%
C. 43,33% e 55,00%
D. 23,33% e 45,00%
E. 23,33% e 55,00%
Justifique sua resposta:
Resposta:
Caixa A= 20 Canetas, dessas 7 são defeituosas
Caixa B= 12 Canetas, dessas 4 são defeituosas
P[canetas boas] =
Probabilidade [canetas boas caixa A E canetas boas caixa B] =
P(canetas boas em A) = = 13/20=0,65 ou 65%
P(canetas boas em B)= =8/12=0,66666666ou 66,67%
Probabilidade [canetas boas caixa A E canetas boas caixa B]=0,65*0,66666666=0,43333333*100=43,33%
Resp. 1: As probabilidades de que ambas não sejam defeituosas são de 43,33%
2- Probabilidade [peça fabricada E peça defeituosa] = ??
Qual a probabilidade de que uma caneta escolhida ao acaso seja perfeita e a outra não?
Obs. Com a resolução da 1ª parte sei que a resposta para esse exercício será a B ou a C.
-
tatimamedes
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sex Mar 01, 2013 00:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração de Empresas
- Andamento: cursando
 por young_jedi » Sex Mar 01, 2013 22:57
por young_jedi » Sex Mar 01, 2013 22:57
vamos separar em dois casos
primeiro: se a caneta defeituosa for retirada da caixa de 20 canetas e caneta boa da caixa de 12
a probabilidade deste evento é

agora o contrario se a caneta boa for retirada da caixa de 20 canetas e a caneta defeituosa da caixa de 12
a probabilidade deste evento é
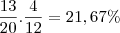
somando os dois
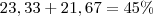
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por tatimamedes » Sex Mar 01, 2013 23:11
por tatimamedes » Sex Mar 01, 2013 23:11
Entendi. Sua explicação foi muito boa.
Eu resolvi assim:
1- P[canetas boas] =
Probabilidade [canetas boas caixa A E canetas boas caixa B] =
P(canetas boas em A) = = 13/20=0,65 ou 65%
P(canetas boas em B)= =8/12=0,66666666ou 66,67%
Probabilidade [canetas boas caixa A E canetas boas caixa B]=0,65*0,66666666=0,43333333*100=43,33%
Resp. 1: As probabilidades de que ambas não sejam defeituosas são de 43,33%
2- Probabilidade [peça fabricada E peça defeituosa] =
Probabilidade [canetas defeituosas caixa A E canetas boas caixa A]+ Probabilidade [canetas defeituosas caixa B E canetas boas caixa B]=
7/20*13/20=0,35*0,65=0,2275 +
4/12*8/12=0,333333*0,6666666=0,222222 = 0,44972222*100=44,972222=~45%
Resp. 2: As probabilidades de que uma seja perfeita e a outra não são de 45%
Será que o meu raciocínio está errado?
-
tatimamedes
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sex Mar 01, 2013 00:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração de Empresas
- Andamento: cursando
 por young_jedi » Sex Mar 01, 2013 23:22
por young_jedi » Sex Mar 01, 2013 23:22
a primeira parte esta certo
agora a segunda não entendi porque voce multiplicou as probabilidade de se retirar uma boa da caixa A pela se retirar uma ruim da Caixa A
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por anabatista » Qua Abr 10, 2013 01:42
por anabatista » Qua Abr 10, 2013 01:42
Vamos passo a passo...
primeiro determinamos os eventos
A= caneta da caixa A sem defeito P(A)= 7/20
a= caneta da caixa A com defeito P(a)=13/20
B= caneta da caixa B sem defeito P(B)= 4/12
b= caneta da caixa B com defeito P(b) = 8/12
A primeira parte está correta!
QUando se fala em probabilidade de ocorrer X e Y, ao mesmo tempo, utiliza-se
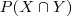
que é dada pelo produto das probabilidades.
Logo a probabilidade de ambas não serem defeituosas é
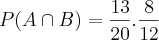
= 43,33%
Parte 2:
Quando se pede para calcular a probabilidade de uma ser defeituosa e outra boa, não se determina de qual caixa vem logo,
a defeituosa pode vir da caixa A OU da caixa B. Quando se usa o termo OU, utiliza-se
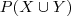
que é dada pela soma das probabilidades.
Então teriamos as seguintes probabilidades,
ter defeito na caneta da caixa A E não ter na B
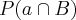
OU (+) não ter defeito na A e ter na B
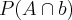
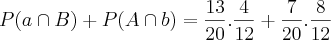
= 45%
Resposta Letra B
-
anabatista
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Seg Abr 08, 2013 23:50
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Estatistica
- Andamento: cursando
 por tatimamedes » Qua Abr 10, 2013 15:43
por tatimamedes » Qua Abr 10, 2013 15:43
Muito obrigada pela ajuda.
-
tatimamedes
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sex Mar 01, 2013 00:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração de Empresas
- Andamento: cursando
Voltar para Dúvidas Pendentes (aguardando novos colaboradores)
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Probabilidades - cálculo probabilidades e condicionada
por carlosmartins » Dom Set 21, 2014 18:58
- 0 Respostas
- 2950 Exibições
- Última mensagem por carlosmartins

Dom Set 21, 2014 18:58
Probabilidade
-
- probabilidades
 por edwilsoncrep » Qui Mar 04, 2010 19:28
por edwilsoncrep » Qui Mar 04, 2010 19:28
- 3 Respostas
- 3274 Exibições
- Última mensagem por edwilsoncrep

Qui Mar 04, 2010 19:49
Estatística
-
- Probabilidades!
por pferraz » Qui Out 27, 2011 22:53
- 3 Respostas
- 7062 Exibições
- Última mensagem por Russman

Qua Dez 23, 2015 22:04
Estatística
-
- Probabilidades
por matematicaead » Qua Nov 16, 2011 13:53
- 1 Respostas
- 2220 Exibições
- Última mensagem por Neperiano

Qua Nov 23, 2011 16:32
Estatística
-
- probabilidades
por cris_leite » Seg Jan 23, 2012 21:17
- 9 Respostas
- 5537 Exibições
- Última mensagem por fraol

Dom Jan 29, 2012 12:41
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



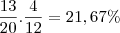
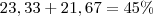

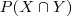 que é dada pelo produto das probabilidades.
que é dada pelo produto das probabilidades.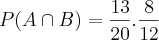 = 43,33%
= 43,33%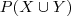 que é dada pela soma das probabilidades.
que é dada pela soma das probabilidades.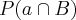 OU (+) não ter defeito na A e ter na B
OU (+) não ter defeito na A e ter na B 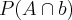
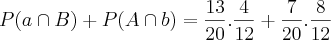 = 45%
= 45%


 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.