 por -Sarah- » Qua Fev 27, 2013 19:08
por -Sarah- » Qua Fev 27, 2013 19:08
Seja x o número cujo logaritmo na base
![\sqrt[3]{9} \sqrt[3]{9}](/latexrender/pictures/32fa931f3d4f8b1110acfdbbe9d2b6d2.png)
vale 0,75. Então

vale:
a) 2
b)
![\sqrt[]{2}-1 \sqrt[]{2}-1](/latexrender/pictures/6c3294e0c67e624ed22baded599501b2.png)
c)
![\sqrt[]{3}-1 \sqrt[]{3}-1](/latexrender/pictures/4b515e5abee7652a0ffbdc40bc203154.png)
d) 0,75
-
-Sarah-
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Sáb Fev 23, 2013 18:20
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Russman » Qua Fev 27, 2013 20:21
por Russman » Qua Fev 27, 2013 20:21
É só resolver a equação
![\log _{\sqrt[3]{9}}\left (x \right )=0,75 \log _{\sqrt[3]{9}}\left (x \right )=0,75](/latexrender/pictures/27dfa7a00a58bbb221b77d598bc8dff3.png)
.
Já tentou?
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por -Sarah- » Qui Fev 28, 2013 16:23
por -Sarah- » Qui Fev 28, 2013 16:23
Sim, mas sem sucesso... Se você pudesse responde-la em detalhes eu agradeceria.
-
-Sarah-
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Sáb Fev 23, 2013 18:20
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Cleyson007 » Qui Fev 28, 2013 16:39
por Cleyson007 » Qui Fev 28, 2013 16:39
Russman desculpe responder um tópico que você iniciou acompanhando, mas como estou online..
log
(?9 ) x = 0,75
log
(?9 ) x = 75/100 ---> log
(?9 ) x = 3/4
![x={(\sqrt[3]{9})}^{\frac{3}{4}} x={(\sqrt[3]{9})}^{\frac{3}{4}}](/latexrender/pictures/166bbdc1ef1287abcfd47aa1dbc991f5.png)
![x={(\sqrt[3]{3^2})}^{\frac{3}{4}} x={(\sqrt[3]{3^2})}^{\frac{3}{4}}](/latexrender/pictures/7a0824ace82eb2674a9aac7e7a3534bb.png)
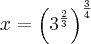
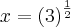
![x=\sqrt[]{3} x=\sqrt[]{3}](/latexrender/pictures/523b5ee3434676b965de6142a602f32d.png)
Voltando ao problema:
![x^2-1 = \left(\sqrt[]{3} \right)^2-1\Rightarrow3-1=2 x^2-1 = \left(\sqrt[]{3} \right)^2-1\Rightarrow3-1=2](/latexrender/pictures/55f708394b3fad07ba4524032f4c94ee.png)
Qualquer dúvida estou a disposição

Cleyson007
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Russman » Qui Fev 28, 2013 22:23
por Russman » Qui Fev 28, 2013 22:23
É isso aí! (:
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por -Sarah- » Seg Mar 04, 2013 20:09
por -Sarah- » Seg Mar 04, 2013 20:09
Ah! Eu não tinha transformado o 9 em
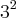
...

Muito Obrigada!

-
-Sarah-
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Sáb Fev 23, 2013 18:20
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[3]{9} \sqrt[3]{9}](/latexrender/pictures/32fa931f3d4f8b1110acfdbbe9d2b6d2.png) vale 0,75. Então
vale 0,75. Então  vale:
vale:![\sqrt[]{2}-1 \sqrt[]{2}-1](/latexrender/pictures/6c3294e0c67e624ed22baded599501b2.png)
![\sqrt[]{3}-1 \sqrt[]{3}-1](/latexrender/pictures/4b515e5abee7652a0ffbdc40bc203154.png)



![x={(\sqrt[3]{9})}^{\frac{3}{4}} x={(\sqrt[3]{9})}^{\frac{3}{4}}](/latexrender/pictures/166bbdc1ef1287abcfd47aa1dbc991f5.png)
![x={(\sqrt[3]{3^2})}^{\frac{3}{4}} x={(\sqrt[3]{3^2})}^{\frac{3}{4}}](/latexrender/pictures/7a0824ace82eb2674a9aac7e7a3534bb.png)
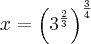
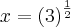
![x=\sqrt[]{3} x=\sqrt[]{3}](/latexrender/pictures/523b5ee3434676b965de6142a602f32d.png)
![x^2-1 = \left(\sqrt[]{3} \right)^2-1\Rightarrow3-1=2 x^2-1 = \left(\sqrt[]{3} \right)^2-1\Rightarrow3-1=2](/latexrender/pictures/55f708394b3fad07ba4524032f4c94ee.png)



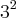 ...
...  Muito Obrigada!
Muito Obrigada! 



 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.