Questões Integral Definida, Áreas e Volumes.

por **walterdavid** » Qui Out 01, 2009 21:21

Boa noite pessoal. Estou com dúvida em algumas questões se puderem me ajudar seria ótimo.

1.resolver pelo teorema fundamental do cálculo
$\int_{-3}^{4}\left | x+1 \right |dx$
no meus livros não constam resolução com módulo entao não sei nem como começar

2
$\int_{1}^{e^{\frac{\Pi }{4}}}\frac{4}{t\left ( 1+ln^2t \right )}dt$
dispensa e

3
$\int_{0}^{1}10^xdx$

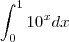
4: encontre os valores de c tal que a área da região limitada pelas parábolas y=x^2 - c^2

e

seja 576.
essa eu já tentei de tudo. mas esto com dificuldades pra enxergar a interseção formada e consequentemente os limites de integração. seria de -c á c? por que para descobrir os limites de int. em uma equação de área faz-se a interseção das equações certo?

agradeço a ajuda
Walter

por **Lucio Carvalho** » Sex Out 02, 2009 14:55

Olá Walter,
Tentarei explicar os exercícios.
No 1º exercício, devemos lembrar que f(x) = |x + 1| =
-(x + 1) se x < -1
(x + 1) se x >= -1

Assim:

$\int_{-3}^{4}|x+1|dx=\int_{-3}^{-1}(-x-1)dx+\int_{-1}^{4}(x+1)dx$

$\int_{-3}^{4}|x+1|dx=2+12,5=14,5$

No 2º exercício, devemos lembrar por integração imediata que:

$\int_{}^{}\frac{f'(x)}{1+{f}^{2}(x)}dx=arctg[f(x)]+k$

Assim:

$\int_{1}^{{e}^{\frac{\pi}{4}}}\frac{4}{t(1+{ln}^{2}t)}dt=4\int_{1}^{{e}^{\frac{\pi}{4}}}\frac{\frac{1}{t}}{1+{ln}^{2}t}dt$

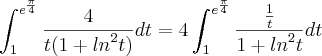
$\int_{1}^{{e}^{\frac{\pi}{4}}}\frac{4}{t(1+{ln}^{2}t)}dt=4.arctg[ln({e}^{\frac{\pi}{4}})]-4.arctg[ln(1)]$

$\int_{1}^{{e}^{\frac{\pi}{4}}}\frac{4}{t(1+{ln}^{2}t)}dt=4.arctg(\frac{\pi}{4})$

No terceiro exercício, sabemos por integração imediata que:

$\int_{}^{}{a}^{x}.ln(a)={a}^{x}+k$

Assim:

$\int_{0}^{1}{10}^{x}dx=\frac{1}{ln(10)}\int_{0}^{1}{10}^{x}.ln(10)dx$

$\int_{0}^{1}{10}^{x}dx=\frac{1}{ln(10)}(10-1)=\frac{9}{ln(10)}$

No 4º exercício, primeiro determinamos os limites de integração fazendo:

${x}^{2}-{c}^{2}={c}^{2}-{x}^{2}$

x=-c

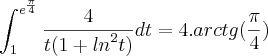
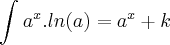
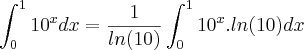
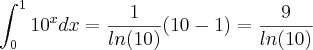
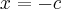(limite inferior)
x=c

(limite superior)

Em seguida:

$\int_{-c}^{c}[({c}^{2}-{x}^{2})-({x}^{2}-{c}^{2})]dx=576$

$\int_{-c}^{c}(-2{x}^{2}+2{c}^{2})dx=576$

$(\frac{-2{c}^{3}}{3}+2{c}^{3})-(\frac{2{c}^{3}}{3}-2{c}^{3})=576$

$c=\sqrt[3]{216}=6$

Espero ter ajudado e até breve!

por **walterdavid** » Ter Out 06, 2009 20:33

nos cara ajudo demais da conta
muito obrigado mesmo

Questões Integral Definida, Áreas e Volumes.

Questões Integral Definida, Áreas e Volumes.

Questões Integral Definida, Áreas e Volumes.

Re: Questões Integral Definida, Áreas e Volumes.

Re: Questões Integral Definida, Áreas e Volumes.

Quem está online