![\lim_{x\to0}\left[\frac{1}{x}+lnx \right] \lim_{x\to0}\left[\frac{1}{x}+lnx \right]](/latexrender/pictures/2d844ef6ee435deda50470d8d9383b89.png) , não estou conseguindo resolver esse limite por l'hospital a resposta é infinito mas só encontro zero.
, não estou conseguindo resolver esse limite por l'hospital a resposta é infinito mas só encontro zero.alguém me ajude por favor

![\lim_{x\to0}\left[\frac{1}{x}+lnx \right] \lim_{x\to0}\left[\frac{1}{x}+lnx \right]](/latexrender/pictures/2d844ef6ee435deda50470d8d9383b89.png) , não estou conseguindo resolver esse limite por l'hospital a resposta é infinito mas só encontro zero.
, não estou conseguindo resolver esse limite por l'hospital a resposta é infinito mas só encontro zero.
matmatco escreveu:, não estou conseguindo resolver esse limite por l'hospital a resposta é infinito mas só encontro zero.
alguém me ajude por favor
 (e portanto x < 0), temos que
(e portanto x < 0), temos que 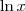 não está definido. O que podemos calcular na verdade é:
não está definido. O que podemos calcular na verdade é:
 . Para aplicar a Regra de L'Hospital, precisamos reescrever esse limite na forma
. Para aplicar a Regra de L'Hospital, precisamos reescrever esse limite na forma 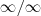 (ou ainda, 0/0).
(ou ainda, 0/0).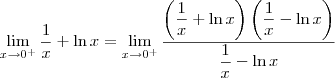
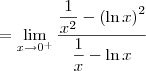
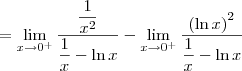
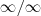 . Desse modo, podemos aplicar a Regra de L'Hospital em cada um deles.
. Desse modo, podemos aplicar a Regra de L'Hospital em cada um deles.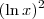 com
com 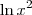 .
.
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes

 .
.



