MAT0120
Regras do fórum
- Não envie somente enunciados de problemas, informe suas tentativas e dificuldades!
Queremos que a "ajuda" represente um trabalho interativo, pois saber especificar a dúvida exige estudo.
Serão desconsiderados tópicos apenas com enunciados, sem interação. Nosso objetivo não é resolver listas de exercícios;
- Para não haver má interpretação em suas postagens, especialmente na precedência das operações, utilize LaTeX, podendo ser a partir do botão "editor de fórmulas".
Bons estudos!
 por Diofanto » Dom Fev 24, 2013 20:57
por Diofanto » Dom Fev 24, 2013 20:57
Não consigo resolver a seguinte questão do livro Álgebra Moderna (Hygino H. Domingues e Gelson Iezzi) 4ª Ed
Pág. 98 Ex 63.
Seja

, dada pela lei:
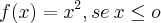
![f(x)={\sqrt[3]{x}, se\: x > 0 f(x)={\sqrt[3]{x}, se\: x > 0](/latexrender/pictures/a2455b4dc99eef6a1e241fb2db5b1487.png)
Determine:
![a)f\left(\left[-1,8 \right] \right) a)f\left(\left[-1,8 \right] \right)](/latexrender/pictures/afa68d887cebc422e84558482b3ebcfe.png)
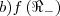
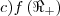
![d){f}^{-1}\left(\left[1,16 \right] \right) d){f}^{-1}\left(\left[1,16 \right] \right)](/latexrender/pictures/989317d84c47c73d21304d4074c40281.png)
![d){f}^{-1}\left(\left[-1,16 \right] \right) d){f}^{-1}\left(\left[-1,16 \right] \right)](/latexrender/pictures/efbf1bac123e281488ee54e8197a4200.png)
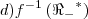
Se for possível, queria a resolução de apenas uma como exemplo, e uma explicação de como fazer as outras.
Minha dúvida é, por exemplo na a), fiz o gráfico das duas funções:

Não sei cmo fazer pra ele aparecer aqui.
Enfim, fiz o grafico, mas n sei cmo estudar ele.
SE puderem me ajudar agradeço.
" A Matemática é o alfabeto com o qual Deus fez o Universo"
-

Diofanto
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Qui Set 20, 2012 15:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura e Bacharelado em Matemática
- Andamento: cursando
-
 por Russman » Dom Fev 24, 2013 22:01
por Russman » Dom Fev 24, 2013 22:01
Você tem uma função contínua definida por partes!
Veja o gráfico:
ScreenHunter_01 Feb. 24 20.58.gif
.
Agora, para calcular a imagem dos intervalos basta que você redimensione esse gráfico de acordo com o intervalo em questão.
Você não está autorizado a ver ou baixar esse anexo.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Álgebra I para Licenciatura
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Álgebra Linear] Núcleo e Imagem
por RafaelPereira » Seg Mar 04, 2013 15:39
- 0 Respostas
- 1598 Exibições
- Última mensagem por RafaelPereira

Seg Mar 04, 2013 15:39
Álgebra Linear
-
- Álgebra Linear Matriz Inversa
por Daniel Serra » Dom Set 15, 2013 13:33
- 0 Respostas
- 1852 Exibições
- Última mensagem por Daniel Serra

Dom Set 15, 2013 13:33
Álgebra Linear
-
- [Função Inversa] Dúvida sobre como calcular a inverso
por Richard Oliveira » Sex Nov 04, 2011 16:36
- 3 Respostas
- 4438 Exibições
- Última mensagem por Richard Oliveira

Sáb Nov 05, 2011 02:54
Funções
-
- QUESTÃO DE DOMÍNIO E IMAGEM
 por Matpas » Qui Ago 27, 2015 16:21
por Matpas » Qui Ago 27, 2015 16:21
- 1 Respostas
- 1246 Exibições
- Última mensagem por nakagumahissao

Sex Ago 28, 2015 20:06
Funções
-
- Livro sobre Álgebra I
por Caeros » Seg Mar 21, 2011 00:38
- 7 Respostas
- 8472 Exibições
- Última mensagem por Diofanto

Qui Jan 31, 2013 21:21
Álgebra I para Licenciatura
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 , dada pela lei:
, dada pela lei: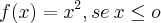
![f(x)={\sqrt[3]{x}, se\: x > 0 f(x)={\sqrt[3]{x}, se\: x > 0](/latexrender/pictures/a2455b4dc99eef6a1e241fb2db5b1487.png)
![a)f\left(\left[-1,8 \right] \right) a)f\left(\left[-1,8 \right] \right)](/latexrender/pictures/afa68d887cebc422e84558482b3ebcfe.png)
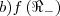
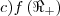
![d){f}^{-1}\left(\left[1,16 \right] \right) d){f}^{-1}\left(\left[1,16 \right] \right)](/latexrender/pictures/989317d84c47c73d21304d4074c40281.png)
![d){f}^{-1}\left(\left[-1,16 \right] \right) d){f}^{-1}\left(\left[-1,16 \right] \right)](/latexrender/pictures/efbf1bac123e281488ee54e8197a4200.png)
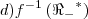



 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.