 por MarlonMO250 » Dom Fev 24, 2013 16:37
por MarlonMO250 » Dom Fev 24, 2013 16:37
Olá, estou começando a estudar derivadas e estou com uma duvida meio basica em uma questão, no caso 3/x², no formato: f'(x)= lim.......f(x+?x) - f(x), como eu resolvo essa derivada nesse modelo?
...........................................................................................................................................................?x ? 0.........?x
-
MarlonMO250
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Dom Fev 03, 2013 11:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Computação
- Andamento: cursando
 por 11121EEL061 » Dom Fev 24, 2013 18:41
por 11121EEL061 » Dom Fev 24, 2013 18:41
Olá, aqui está minha resolução, vou trocar ?x ? 0 por h ? 0, para facilitar.
f(x) = 3/x²
f '(x) = lim(h ? 0) f(x+h) - f(x) / h
= lim(h ? 0) (3/(x+h)² + 3/x²)/h
= lim(h ? 0) (3x²-3(x+h)²)/(hx²(x+h)²)
= lim(h ? 0) (3x² -3x² -6xh -3h²)/(hx²(x²+2xh+h²)
= lim(h ? 0) h(-6x-3h)/hx²(x²+2xh+h²)
= lim(h ? 0) (-6x-3h)/(x^4 +2x³h+2x²h²)
= lim(h ? 0) (-6/x(x³+2x²h+2xh²)) + (-3h/(x^4 +2x³h+2x²h²)) Como h tende a zero, é só substituir zero no lugar de h.
= -6/x³
Espero ter ajudado. Fica com Deus.
-
11121EEL061
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Dom Fev 24, 2013 18:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por MarlonMO250 » Dom Fev 24, 2013 19:24
por MarlonMO250 » Dom Fev 24, 2013 19:24
Cara, primeiro agradeço imensamente pela resposta, mas voltando ao problema, porque você pasou de

pra

, porque a troca de sinal?
e depois, como foi disso:

pra
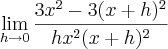
?
-
MarlonMO250
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Dom Fev 03, 2013 11:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Computação
- Andamento: cursando
 por Russman » Dom Fev 24, 2013 20:21
por Russman » Dom Fev 24, 2013 20:21
As passagens as quais você tem dúvida são simples desenvolvimento algébrico.
Veja que
![[tex]\frac{a}{b} + \frac{c}{d} = \frac{ad+cb}{db} [tex]\frac{a}{b} + \frac{c}{d} = \frac{ad+cb}{db}](/latexrender/pictures/ea95abac7a5b4e09d06ff8b10fd1e632.png)
[/tex],
de forma que

"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Matémática básica
por drea70br » Dom Out 04, 2009 20:59
- 1 Respostas
- 6171 Exibições
- Última mensagem por Elcioschin

Dom Out 04, 2009 21:10
Álgebra Elementar
-
- Operação básica
por Fernanda Lauton » Qui Jun 17, 2010 15:40
- 11 Respostas
- 6467 Exibições
- Última mensagem por Fernanda Lauton

Seg Jun 21, 2010 18:13
Álgebra Elementar
-
- Inequação Básica
por ptt » Seg Jun 21, 2010 20:38
- 2 Respostas
- 2375 Exibições
- Última mensagem por MarceloFantini

Ter Jun 22, 2010 00:56
Álgebra Elementar
-
- Equação básica
por SaraSFT » Ter Jul 03, 2012 06:12
- 1 Respostas
- 1487 Exibições
- Última mensagem por MarceloFantini

Ter Jul 03, 2012 22:23
Matemática Financeira
-
- Dúvida básica
por SaraSFT » Ter Jul 03, 2012 06:33
- 1 Respostas
- 1318 Exibições
- Última mensagem por MarceloFantini

Ter Jul 03, 2012 22:31
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 pra
pra  , porque a troca de sinal?
, porque a troca de sinal?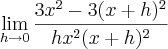 ?
?![[tex]\frac{a}{b} + \frac{c}{d} = \frac{ad+cb}{db} [tex]\frac{a}{b} + \frac{c}{d} = \frac{ad+cb}{db}](/latexrender/pictures/ea95abac7a5b4e09d06ff8b10fd1e632.png) [/tex],
[/tex],
